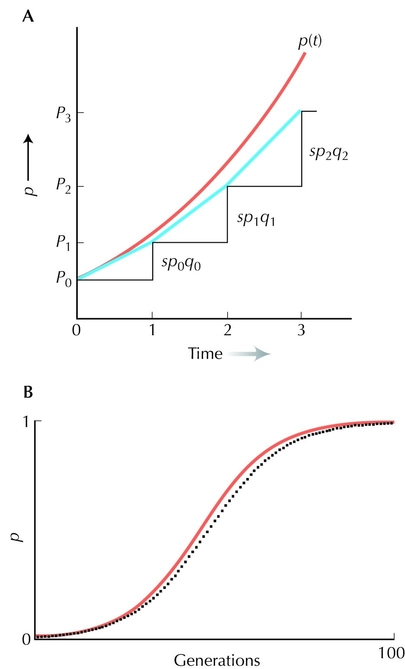

Figure 28.7. A differential equation is a good approximation to a discrete recursion when change is gradual. (A) The series of triangles shows the solution to the recursion pt + 1 = pt + sptqt, for generations 0, 1, 2, ... . The continuous red curve is the solution to dp/dt = sp(t)q(t). This has the same slope at time t = 0, when p(0) = p0. Compare the slope of the red curve with the diagonal line, which has slope sp0q0. However, because the differential equation allows for a continuous acceleration (i.e., an upward curve) as allele frequency increases, it increases slightly faster than the discrete recursion (black steps). (B) The discrete recursion (black dots) with WP/WQ = 1.1 compared with the continuous solution (red curve) to dp/dt = spq with s = 0.1; allele frequency is initially 0.01. Agreement is close at first, but errors build up over time; nevertheless, the error is never more than 4%.
| © 2007-2010 by Cold Spring Harbor Laboratory Press. All rights reserved. |
| The reproduction, modification, storage in a retrieval system, or retransmission, in any form or by any means, electronic, mechanical, or otherwise, for reasons other than personal, noncommercial use is strictly prohibited without prior written permission. You are authorized to download one copy of the material on this Web site for personal, noncommercial use only. The material made available on this Web site is protected by United States copyright laws and is provided solely for the use of instructors in teaching their courses and assessing student learning. Dissemination or sale of any of this material, as a whole or in parts (including on the World Wide Web), is not permitted. All users of these materials and visitors to this Web site are expected to abide by these restrictions. Requests for permission for other uses of this material should be directed to Cold Spring Harbor Laboratory Press, 1 Bungtown Road, Cold Spring Harbor, NY 11724 or submitted via our World Wide Web Site at http://www.cshlpress.com/. |