The Relation between Changes in Quantitative Traits and Changes in Allele Frequency

Suppose that a quantitative trait z is influenced by many genes, labeled i = 1, 2, ..., and each with two alleles (P_i, Q_i). Call the additive effect of the ith gene on the trait α_i. Assuming that the population is diploid, mates at random, and is in linkage equilibrium, we can write the trait mean as a sum of effects of all the loci:

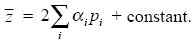
The factor of 2 arises because each individual carries two copies of every gene; and the constant is just the value the trait would have if every locus carried Q alleles. (Without assuming random mating and linkage equilibrium, we cannot describe the population just in terms of allele frequencies.)

Now, the change in trait mean due to selection is just

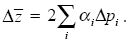
We know that the change in allele frequency at the ith locus is Δp_i = s_ip_iq_i, where the selection coefficient s_i is the difference in relative fitness between the two alleles. If selection is entirely due to differences in the trait, then this is just s_i = β α_i. That is, if substituting P_i for Q_i changes the trait by α_i, then it must change fitness by β α_i. Thus,

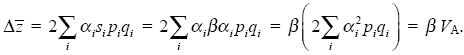
The last step uses the fact that V_A is defined as the variance of additive effects on the trait (p. 393). The important point to take from this derivation is that all of the genetic details about how many genes are involved and how they affect the trait (i.e., all the α_i) are absorbed into V_A, which is a quantity that can be measured without knowing any of the genetics. This allows us to understand how selection affects quantitative traits even though we do not usually know how the underlying genes determine the trait.