Mutation/Selection Balance for a Quantitative Trait
Assume that fitness W depends on the trait z following a Gaussian curve. For simplicity, we set the optimum at 0:

Here, Vs is the variance of the Gaussian curve. The larger Vs is, the wider the range of phenotypes that can survive and the weaker is stabilizing selection (Fig. WN18.9).
Suppose that there is a rare allele that increases the trait by αi. (The subscript i labels this particular allele.) We can assume that individuals homozygous for the other allele (or alleles) are at the optimum, and that individuals carrying one copy of the allele deviate from the optimum by αi and have fitness exp(–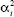 /2Vs). If the deviation is small, this is approximately 1 – /2Vs). If the deviation is small, this is approximately 1 – 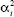 /2Vs (dashed line in Fig. WN18.9). So, the selection against these rare alleles, caused by the deviation of the trait from the optimum, is just si = /2Vs (dashed line in Fig. WN18.9). So, the selection against these rare alleles, caused by the deviation of the trait from the optimum, is just si = 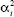 /2Vs. In a mutation selection balance, the allele frequency is pi = µi/si = 2 Vsµi/ /2Vs. In a mutation selection balance, the allele frequency is pi = µi/si = 2 Vsµi/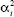 ). ).
With two alleles at each locus, the additive genetic variance is VA = 2Σi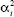 piqi. Because the allele is assumed to be rare, qi ~ 1. Substituting the allele frequency pi we see that the allelic effect piqi. Because the allele is assumed to be rare, qi ~ 1. Substituting the allele frequency pi we see that the allelic effect 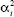 cancels, giving cancels, giving
VA = 4VsΣiµi = 2UVs,
where U = 2Σiµi is the total rate of mutation to alleles affecting the trait per diploid genome.
Here, we have assumed that all the selection on the allele is due to stabilizing selection on the trait. If pleiotropy is extensive, we can just say that the selection against allele i is si and is determined by factors that have nothing to do with the effect on the trait αi. Then, substituting the allele frequency pi = µi/si into the formula for the additive genetic variance gives
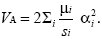
But, we saw in Chapter 14 (p. 410) that the trait variance generated by mutation in each generation is VM = 2Σiµi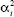 . Hence . Hence
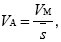
where 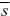 is the average selection coefficient weighted toward alleles with large effects on the trait and small effects on fitness. is the average selection coefficient weighted toward alleles with large effects on the trait and small effects on fitness.
|

