Measuring Distortions in the Pattern of Neutral Variation

If a favorable mutation fixes in the population or if the population has increased in size following a population bottleneck, then the genealogy will look like a star; that is, ancestral lineages will tend to coalesce during the brief selective sweep or at the population bottleneck. Subsequent mutations will therefore be found only in a single lineage and there will be an excess of rare variants (Fig. 19.15A). In contrast, if population size is constant, then most coalescence events will occur much more recently than the common ancestor and so mutations will tend to be represented several times in the sample (Fig. 19.15B).

How can we measure such distortions in the pattern of neutral genetic variation? The most widely used approach is to compare different estimates of the fundamental parameter, θ = 4N_eµ. One estimate, θ_π, is given by the nucleotide diversity π, which is just the average proportions of sites that differ between a random pair of sequences. (For a random mating diploid organism, this is just the heterozygosity; see Chapter 13 [p. 363].) Watterson (1978) proposed an alternative estimate θ_W, which is proportional to the number of segregating sites seen in the sample. Under the neutral theory, these two estimates are expected to be equal (θ_π = θ_W). Therefore, Tajima (1989) suggested that distortions from neutrality could be measured by a statistic D, which is equal to the difference between them divided by the standard deviation (s.d.) of this difference, D = (θ_π – θ_W)/s.d. Rare variants will count toward the number of segregating sites, but will contribute little to pairwise differences. Thus, an excess of rare variants leads to negative values of D.

Both population bottlenecks and selective sweeps lead to negative Tajima’s D. However, the effects of a selective sweep can be distinguished if an outgroup is available, so that the direction of changes can be determined. Fay and Wu (2000) proposed using an estimate θ_H, which is proportional to the homozygosity of derived mutations (i.e., to mutations that occurred in the ancestry of the sample in question and that are not found in the outgroup). θ_H is equal to θ_π and θ_W under the standard neutral theory, but is larger if a selective sweep has carried derived mutations to high frequency. Thus, a statistic H = (θ_π – θ_W)/s.d., analogous to Tajima’s D, can be used specifically to detect selective sweeps that have recently finished (Fig. 19.23).

The alternative measures of diversity, θ_π, θ_W, and θ_H, can be calculated from a list, S_i, of the number of variants that appear 1, 2, 3, ... times in the sample in a sample of n genes. For example, in Figure WN19.3A, S₁ = 4, S₂ = 2, S₃ = 5; in Figure WN19.3B, S₁ = 11; and in Figure WN19.3C, S₁ = 5, S₂ = 1, and S₄ = 5; n = 6. Then

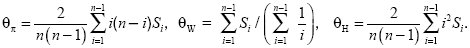
The three estimates θ_π, θ_W, and θ_H are shown in the simulation of Figure WN19.4. Near the selected locus, there is almost no variation and so all three are near to 0. At the edges of this region, there is some variation, and as expected θ_H is substantially increased, because the selective sweep has raised previously rare variants to unexpectedly high frequency (red line). In contrast, θ_W and θ_π (blue and black lines), which determine Tajima’s D, are much less sensitive to the selective sweep. A similar pattern is seen around the Duffy locus (p. 536), where selection has fixed a malaria-resistant allele in West Africa. There, although Tajima’s D is not negative, Fay and Wu’s H statistic is significant, indicating that previously rare variants have hitchhiked to high frequency along with the resistance allele.