A Branching Process in Two Demes
An allele is selected against in one deme, and favored in the other, as in the deterministic model of Box 28.3. If a single copy is introduced into the first deme, it can still migrate to the other deme and increase there. Thus, there is some chance that the gene can invade, but this chance is lower if it is introduced into the first deme versus the second deme. Let the probabilities of survival of a single gene introduced into demes 1, 2 be P1, P2, respectively, where P1 < P2. The probabilities of loss are Q1 = 1 – P1, Q2 = 1 – P2.
As before, we solve the problem by following what can happen to a single copy of the new allele in the next generation. If it starts in deme 1, it has a chance (1 – m) of staying there, and producing, on average, λ1 = 1 – s offspring copies. There is a chance m that it will move to the other deme, in which case it will produce, on average, λ2 = 1 + s copies. We assume a Poisson distribution of offspring number. As before, the crucial step is to see that the chance that the k offspring copies are all lost is Q1k if they are in deme 1 and Q2k if they are in deme 2. Thus,
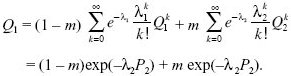
When s is small, the probability of survival will be small, and so we can simplify this using exp(–x) ~1 – x + x2/2:
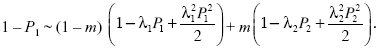
Setting λ1 = 1 – s, λ2 = 1 + s and assuming that m, s, P1, P2 are small and of the same order, we have
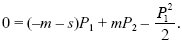
Similarly for a gene that starts in the other deme,
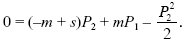
We can see that when migration is very low (m << s), there is little chance that an allele in deme 1 can get to deme 2 before being eliminated by selection, so that P1 << P2. The second equation then simplifies to 0 ~ sP2 – P22/2, so that P2 ~ 2s, as in a single isolated deme. At the other extreme, when migration is high (m >> s), the pair of demes act as one, so that on average the allele has no selective advantage or disadvantage. Thus, with high migration, P1 ~ P2 ~ 0. These two limits can be seen at the left and right of Figure WN28.4, which plots numerical solutions of the pair of equations above against m/s.
|

