Properties of the Coalescent Process

If we trace back the ancestry of two genes, there is a chance of 1/2N_e per generation that they will coalesce. Thus, the time until coalescence follows an exponential distribution with mean T₂ = 2N_e generations (Table 28.1). If there are k genes, then there are k(k – 1)/2 pairs of lineages which could coalesce (three possible pairs with k = 3, six pairs with k = 4, and so on). Thus, the time until the first coalescence follows an exponential distribution with mean T_k = 4N_e/(k(k – 1)). We can find the expected time T_MRCA until the k lineages have coalesced in the most recent common ancestor (MRCA) by adding up the expected time to go from k down to k – 1, from k – 1 down to k – 2, and so on:

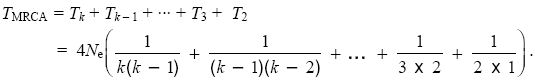
Now, 1/(k(k – 1)) = (1/(k – 1) – 1/k). This leads to a much simpler formula:

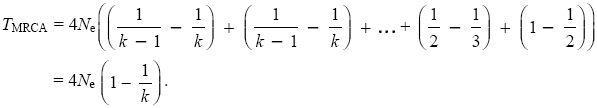
Even with very many lineages (i.e., when k is large), the average time to go down to two lineages is 2N_e, followed by another 2N_e generations to go down to the most recent common ancestor. This is because coalescence is extremely rapid at first, but it then slows down (see Fig. 15.8A).

Other properties of the coalescent process can be found in the same way. For example, the total length of the genealogy (i.e., the total time spanned by all the lineages leading down from the common ancestor to the sample of k genes) is twice the time during which there are two lineages, plus three times the time during which there are three, and so on. The average length is therefore

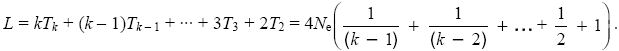
This is close to 4N_elog_e(1.78k). This result is important, because it determines the average number of mutations that will occur somewhere in the genealogy and will therefore appear as polymorphisms or segregating sites.