Chapter 16 Notes

Population Structure

Gene Flow

Natural Populations Are Not Single Well-Mixed Gene Pools

A classic example of polymorphism is the banding patterns in the snail Cepaea nemoralis, one of the few such examples before molecular markers became available. Jones et al. (1977) review the multiple explanations for spatial variation in banding pattern; for a more recent account, incorporating molecular data, see Davison and Clarke (2000).

The example of Figure 16.1B,C is from Ochman et al. (1983). Shell polymorphism is correlated both with temperature (as in Fig. 16.1B) and with camouflage: in some areas at least, shells tend to match their background. However, shell color and banding also sometimes show “area effects,” such as those illustrated for allozyme frequencies in Figure 16.1C, in which large patches show distinct combinations of allele frequencies.

The Rate of Diffusion of Genes Is Measured by σ²

In two dimensions, the distance moved by a gene is measured along some particular axis (x, say). The rate of gene flow in that direction is measured by the variance of that component of distance ( = E[x²], say). The variance of the total distance moved is the sum of the variances in the two directions. This is because, by the Pythagorean theorem, the total distance moved, d, is given by d² = x² + y². Thus, the variance of the distance moved is the sum of contributions from movements along the x and y axes (E[d²] = E[x²] + E[y²] = + 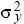). In this chapter, we use σ² to denote the variance along the axis of interest (, say). For example, this might be the distance measured in the direction of a cline.

Dobzhansky and Wright (1943, 1947) made some of the first large-scale measurements of gene flow and were the first to relate this measurement to patterns of genetic variation—in their work, to variation in the frequency of recessive lethals. The history of their collaboration is described by Lewontin et al. (1981), together with reprints of their classic papers.

Coyne et al. (1982) give a nice example of long-distance movements of Drosophila to isolated oases in the Mojave desert.

Diffusion Is a Slow Process

Dispersal rates in Podisma pedestris were measured by Barton and Hewitt (1982); the chromosomal cline was described by Barton and Hewitt (1981).

Gene Flow Interacts with Other Evolutionary Forces

Geographic Variation Is Generated by Random Genetic Drift

For detailed analysis of the interaction between drift and gene flow, see Rousset (2003). The classic mathematical analysis was done by Malécot (1948, 1969).

Hanski and Gilpin (1996) and Hanski (1999) review the ecology and evolution of metapopulations, with emphasis on the implications for conservation of endangered species.

F_ST Is a Standardized Measure of the Genetic Variation between Demes

For discussions of estimation of Wright’s F_ST, see Weir and Cockerham (1984), Weir (1996), and Slatkin and Barton (1990). Q_ST is discussed by McKay and Latta (2002) and Latta (2003), who also review data from nature.

Selection can be detected by comparing F_ST across genes: Higher F_ST may be caused by diversifying selection. A good example comes from the periwinkle, Littorina saxatalis (Using F_ST to Detect Selection in the Periwinkle, Littorina saxatalis). The same approach has been used in comparisons across the human genome to indicate genes that may be selected differently on different continents (see Fig. 26.11).

Detecting selection by comparing the extent of between- and within-population divergence, as measured by F_ST, is similar to the McDonald–Kreitman (Box 19.1) test, which compares divergence within and between species.

The Population as a Whole Drifts Slowly

Whitlock and Barton (1997) review the theory relating to the rate of drift of whole metapopulations.

Frost et al. (2001) describe fine-scaled genetic variation in HIV.

Rates of Gene Flow Can Be Estimated from F_ST

Morjan and Rieseberg (2004) review estimates of F_ST (see Table 16.2).

In animals, F_ST will be lower for mitochondrial genes than for nuclear genes if females move less than males, simply because mitochondria are inherited only through females. The converse applies to the Y chromosome, which is passed down only through males. As well as these differences in gene flow (m), the effective population sizes also differ between genes that are inherited in different ways.

Whitlock and McCauley (1999) criticize the naive inference of Nm from F_ST.

Genealogies in Structured Populations

Genealogies Are Distorted by Population Structure

Charlesworth et al. (2003) review the effects of population subdivision on gene genealogies. This theory carries over from the “classical” results of Wright, Malécot, and others, which are framed in terms of identity by descent or variance in allele frequency.

Wright (1943) introduced neighborhood size. F_ST for two-dimensional populations was given explicitly in the form 1/(1 + C Nb) by Malécot (see Malécot 1948; Charlesworth et al. 2003).

The Relation between Genes from Different Places Reflects Their History: Phylogeography

Phylogeography has been developed primarily by Avise and colleagues (see, e.g., Avise 1998, 2004).

Irwin (2002) described mtDNA genealogies in greenish warblers that suggest a separation of the population but also showed that such patterns can often arise by chance. Knowles and Maddison (2002) criticize qualitative inference from genealogies and, in particular, Templeton’s (1998) method of “nested clade analysis.” See Templeton’s (2004) reply.

Mixing of Populations Generates Linkage Disequilibria

The analysis of hybridization between red and sika deer is from Goodman et al. (1999).

Estimates of gene flow in Bombina are from Szymura and Barton (1991); see also Barton and Gale (1993).

References

Avise J.C. 1998. The history and purview of phylogeography: A personal reflection. Mol. Ecol. 7: 371–379.

Avise J.C. 2004. Molecular markers, natural history and evolution. Sinauer Press, Sunderland, Massachussetts.

Barton N.H. and Hewitt G.M. 1981. A chromosomal cline in the grasshopper Podisma pedestris. Evolution 35: 1008–1018.

Barton N.H. and Gale K.S. 1993. Genetic analysis of hybrid zones. In Hybrid zones and the evolutionary process (ed. R. G. Harrison), pp. 13–45. Oxford University Press, Oxford.

Barton N.H. and Hewitt G.M. 1982. A measurement of dispersal in the grasshopper Podisma pedestris (Orthoptera: Acrididae). Heredity 48: 237–249.

Charlesworth B., Charlesworth D., and Barton N.H. 2003. The effects of genetic and geographic structure on neutral variation. Annu. Rev. Ecol. Syst. 34: 99–125.

Coyne J.A., Boussy I.A., Prout T., Bryant S.H., Jones J.S. et al. 1982. Long-distance migration of Drosophila. Am. Nat. 119: 589–595.

Davison A. and Clarke B. 2000. History or current selection? A molecular analysis of “area effects” in the land snail Cepaea nemoralis. Proc. Biol. Sci. 267: 1399–1405.

Dobzhansky T. and Wright S. 1943. Genetics of natural populations. X. Dispersion rates in Drosophila pseudoobscura. Genetics 28: 304–340.

Dobzhansky T. and Wright S. 1947. Genetics of natural populations. XV. Rate of diffusion of a mutant gene through a population of Drosophila pseudoobscura. Genetics 32: 303–324.

Frost S.K., Dumaurier M.J., Wain-Hobson S., and Leigh Brown A.J. 2001. Genetic drift and within-host metapopulation dynamics of HIV-1 infection. Proc. Natl. Acad. Sci. 98: 6975–6980.

Goodman S.J., Barton N.H., Swanson G., Abernethy K., and Pemberton J.M. 1999. Introgression through rare hybridisation: A genetic study of a hybrid zone between red and sika deer (genus Cervus), in Argyll, Scotland. Genetics 152: 355–371.

Hanski I. 1999. Metapopulation ecology. Oxford University Press, Oxford.

Hanski I. and Gilpin M. 1996. Metapopulation biology: Ecology, genetics and Evolution. Academic Press, San Diego.

Heller J. 1976. The effects of exposure and predation on the shell of two British winkles. J. Zool. Lond. 179: 201–213.

Hull S.L., Grahame J., and Mill P.J. 1996. Morphological divergence and evidence for reproductive isolation in Littorina saxatilis (Olivi) in northeast England. J. Molluscan Stud. 62: 89–99.

Irwin D.E. 2002. Phylogeographic breaks without geographic barriers to gene flow. Evolution 56: 2383–2394.

Jones J.S., Leith B.H., and Rawlings P. 1977. Polymorphism in Cepaea: A problem with too many solutions? Annu. Rev. Ecol. Syst. 8: 109–143.

Knowles L.L. and Maddison W.P. 2002. Statistical phylogeography. Mol. Ecol. 11: 2623–2635.

Latta R.G. 2003. Gene flow, adaptive population divergence and comparative population structure across loci. New Phytol. 161: 51–58.

Lewontin R.C., Moore J.A., Provine W.B., and Wallace B. 1981. Dobzhansky’s “Genetics of natural populations” I–XLIII. Columbia University Press, New York.

McKay J.K. and Latta R.G. 2002. Adaptive population divergence: Markers, QTL and traits. Trends Ecol. Evol. 17: 285–291.

Malécot G. 1948. Les mathématiques de l’hérédité. Masson et Cie, Paris.

Malécot G. 1969. The mathematics of heredity. W.F. Freeman, San Francisco.

Morjan C.L. and Rieseberg L.H. 2004. How species evolve collectively: Implications of gene flow and selection for the spread of advantageous alleles. Mol. Ecol. 13: 1341–1356.

Ochman H., Jones J.S., and Selander R.K. 1983. Molecular area effects in Cepaea. Proc. Natl. Acad. Sci. 80: 4189–4193.

Rousset F. 2003. Genetic structure and selection in subdivided populations. Princeton University Press, Princeton, New Jersey.

Slatkin M. and Barton N.H. 1990. A comparison of three methods for estimating average levels of gene flow. Evolution 43: 1349–1368.

Szymura J.M. and Barton N.H. 1991. The genetic structure of the hybrid zone between the fire-bellied toads Bombina bombina and B. variegata: Comparisons between transects and between loci. Evolution 45: 237–261.

Templeton A.R. 1998. Nested clade analyses of phylogeographic data: Testing hypotheses about gene flow and population history. Mol. Ecol. 7: 381–397.

Templeton A.R. 2004. Statistical phylogeography: Methods of evaluating and minimising inference errors. Mol. Ecol. 13: 789–809.

Weir B.S. 1996. Genetic data analysis II. Sinauer Press, Sunderland, Massachusetts.

Weir B.S. and Cockerham C.C. 1984. Estimating F statistics for the analysis of population structure. Evolution 38: 1358–1370.

Whitlock M.C. and Barton N.H. 1997. The effective size of a subdivided population. Genetics 146: 427–441.

Whitlock M.C. and McCauley D.E. 1999. Indirect measures of gene flow and migration: F_ST not equal to 1/(4Nm + 1). Heredity 82: 117–125.

Wilding C.S., Butlin R.K., and Grahame J. 2001. Differential gene exchange between parapatric morphs of Littorina saxatilis detected using AFLP markers. J. Evol. Biol. 14: 611–619.

Wright S. 1943. Isolation by distance. Genetics 28: 114–138.