Derivation of Fisher’s Fundamental Theorem of Natural Selection
Fisher’s theorem can be derived very simply, provided we look just at the effects of selection in a random-mating population. Suppose that there are many types in the population; we label them i = 1, 2, 3, ... . The frequency of the ith type is xi, and its fitness is Wi. (It is easiest to think of fitness as the average probability of survival of the ith type.) So, the average fitness is  = ΣixiWi and the frequency of the ith type after selection is = ΣixiWi and the frequency of the ith type after selection is 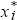 = xiWi/ = xiWi/ . The increase in fitness caused by selection is . The increase in fitness caused by selection is
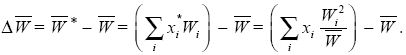
This can be simplified by writing the deviation of fitness from the average by δWi = Wi –  . Then . Then
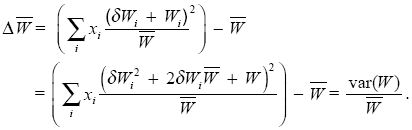
(Notice that the average deviation in fitness, ΣixiδWi, is zero by definition, and Σixi = 1.
Thus, the increase in mean fitness caused by selection is equal to the total variance in fitness divided by the mean. However, this simple derivation only includes the immediate effect of selection. We would like to know the change in mean fitness over a whole generation, including the effects of sexual reproduction. Then, fitnesses will not necessarily stay the same, and genotype frequencies can change as a result of recombination as well as selection. Despite these complications, however, Fisher’s Fundamental Theorem still applies, provided we focus on the change in mean fitness caused by the effects of selection on allele frequencies.
Imagine that many genes influence fitness; now, we label these genes i = 1, 2, 3, ... . For simplicity, assume that the ith gene has two alleles, Pi and Qi, at frequencies pi, qi. If the population is haploid, then for each gene, we can divide the population into two parts: those carrying Pi and those carrying Qi. We can measure the fitness of each part as WPi, WQi; necessarily, the mean fitness is  = piWPi + qiWQi. The change in allele frequency caused by selection is just = piWPi + qiWQi. The change in allele frequency caused by selection is just
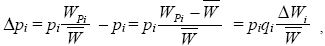
where ΔWi = WPi – WQi. (Recall from Chapter 14 that this is just the difference between the average effect on fitness of the two alleles.) This formula is exact. The change in allele frequency at the ith gene only depends on the difference in fitness between the individuals carrying Pi and those carrying Qi. Moreover, Mendelian inheritance does not alter allele frequencies, and so the above formula gives the change across the whole generation.
What is the change in mean fitness? In general, this is difficult to find, because the fitnesses of each allelic class (WPi, WQi) might change from one generation to the next. Fitnesses of individual genotypes may change as the environment changes, and the average fitness of individuals carrying Pi alleles may change through their association with alleles at other loci. Nevertheless, we can find that part of the increase in mean fitness that is caused by the change in allele frequencies. We know that replacing an individual carrying a Qi allele with one carrying a Pi allele will on average change fitness by ΔWi. So, the net effect on mean fitness of all the changes in allele frequency brought about by selection is
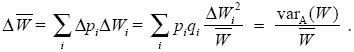
We have that the change in mean fitness is proportional to the sum over genes of piqiΔ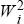 , which for a haploid population is equal to the additive genetic variance in fitness (see Chapter 14, pp. 393–394). , which for a haploid population is equal to the additive genetic variance in fitness (see Chapter 14, pp. 393–394).
Fisher’s Fundamental Theorem is exactly correct in a wide variety of cases; for example, a similar derivation applies for a diploid population and for nonrandom mating. However, it must be interpreted carefully. It states that the increase in mean fitness due to the changes in allele frequency caused by selection is proportional to that part of the variance in fitness that can be attributed to the additive effects of the genes.
|

