|
Problem 17.1
|
| **i) |
A population reproduces asexually in discrete generations and consists of two types (Q, P, say). Type Q produces 1 offspring per generation, whereas P produces on average 1.1 offspring per generation. Initially, P is rare, at frequency p = 10–5. What is the ratio between the frequencies of P and Q after ten generations? HINT 17A After 100 generations? How long will it take for the two types to be equally frequent?
|
| **ii) |
Write down an approximate formula for the rate of change in allele frequency, dp/dt, through continuous time. HINT 17B
|
| ***iii) |
How accurate is this approximation?
|
|
Problem 17.2
A favorable allele with selective advantage s is initially absent (p = 0 at t = 0) but is generated by mutation at a rate μ per generation.
|
| *i) |
Write down a formula for its rate of increase while it is still rare (p << 1). HINT 17C
|
| **ii) |
Show that the solution to this formula is p = (μ/s)(est – 1).
|
| **iii) |
When will the allele reach p = 0.5? Assume that if the allele is not very rare (p >> μ/s), then mutation becomes negligible, so that the solution matches the formula for selection alone; this formula is p = (μ/s)est/(1 + (μ/s)est).
|
| **iv) |
Resistance to a new insecticide can evolve in two ways. A specific amino acid substitution gives strong resistance (and a selective advantage s = 0.1) and arises by mutation at μ = 10–10 per generation. Defects at ten other genes each give weak resistance (and have advantage s = 0.01); these defects arise much more frequently at μ = 10–8 for each of the ten genes. Which form of resistance will evolve first? HINT 17D NOTE 17A
|
|
Problem 17.3
|
| *i) |
The absolute fitness of a haploid population of genotype Q and size N is WQ = 4/(1 + N)2. (N is measured in arbitrary units—millions, for example.) Thus, absolute fitness decreases as the population becomes more crowded. What is the population size at equilibrium, when WQ = 1?
|
| **ii) |
A new allele increases fitness at high density, but reduces it at low density: WP = (3/4)(1 + N) WQ. Sketch a graph of the fitnesses of the two genotypes against population size. HINT 17E
|
| **iii) |
Will allele P invade and fix if it is introduced to a population of Q that is at equilibrium? If it does, what will be the new population size at equilibrium? HINT 17F
|
| **iv) |
If Q and P both start at low density, but with Q much more common than P, what will happen? (A qualitative answer will be enough here.)
|
|
Problem 17.4
An insect larva has an 80% chance of surviving over a year. If it does survive, then it is equally likely to continue as a larva or to metamorphose into an adult. Adults are diploid and reproduce sexually with equal sex ratio; females bear two larvae on average. Both sexes die immediately after breeding.
|
| **i) |
Starting with 100 larvae, follow the numbers of larvae and adults over the next 15 years. Once the population has reached a steady rate of increase, by what factor does it increase each year? What is the ratio of juveniles to adults? HINT 17G
|
| **ii) |
A new allele arises at low frequency. Adult heterozygotes for this allele produce 20% more offspring but have the same rates of survival and metamorphosis. What is the long-term rate of increase of this new allele? (We examine models of age-structured populations further on pp. 562–566 and in the Web Notes.)
|
|
Problem 17.5
A population of ten haploid individuals reproduces as shown in Figure P17.1; two alleles segregate (red, blue).
|
| *i) |
What are the fitnesses of the ten individuals in the first generation? What is the variance in fitness?
|
| **ii) |
The fitness of each individual can be treated as a quantitative trait and described using the methods of Chapter 14. Estimate the average excess for each of the two alleles, in the first generation. What is the additive genetic variance in fitness? HINT 17H
|
| **iii) |
What is the change in mean fitness due to the change in allele frequencies? In other words, what is the predicted mean fitness of the offspring, given the average excess of each allele? Show that this change is related to the additive genetic variance by Fisher’s Fundamental Theorem (see p. 462).
|
| **iv) |
What is the actual change in mean fitness between the two generations shown here? Explain why this is different from the value calculated in iii).
|
|
Problem 17.6
Figure P17.2 shows the reproduction of a population of 20 individuals. Each diploid individual carries a pair of genomes (vertical lines), each with two genes. There are two alleles at each locus (red, blue at the top locus, and green, black at the bottom locus). This question examines Fisher’s Fundamental Theorem, working first at the level of haploid genomes and then at the level of diploid individuals.
|
| *i) |
Write onto Figure P17.2 which gene has been transmitted by which parent. (When the locus is heterozygous, there may be more than one possible answer. Choose one.)
|
| **ii) |
At each locus, find the fitness of each of the 40 genomes (i.e., find how many copies each gene transmits). The fitness of each gene can be treated as a quantitative trait and described using the methods of Chapter 14. What is the variance of fitness across genes at the first locus? At the second? What is the average excess for each of the two alleles at each locus? Considering just these two loci, what is the additive genetic variance in fitness? What is the change in mean fitness due to the change in allele frequencies? In other words, what is the predicted mean fitness of the offspring, given the average excess of each allele? Show that these two are related by Fisher’s Fundamental Theorem. NOTE 17B
|
| **iii) |
We can instead consider diploid individuals; indeed, because we usually do not know which gene is transmitted at meiosis, this is usually what we would do. What is the fitness of each of the 20 diploid individuals? What is the average excess for each allele, the additive genetic variance, and the change in mean fitness due to the change in allele frequencies? Does Fisher’s Fundamental Theorem describe the relationship between these? If not, why not?
|
|
Problem 17.7
An allele P has an effect on fitness that varies with the environment. In environment A, PQ heterozygotes are on average 10% less fit than QQ homozygotes, whereas in environment B, they are twice as fit.
|
| *i) |
Environment A is experienced in nine out of ten generations, and B in one out of ten generations. Can allele P invade a population that is initially predominantly QQ?
|
| *ii) |
Now, suppose that the environment varies in space rather than through time. At the start of each generation, individuals land on a patch that has a 90% chance of being of type A and 10% of type B. After selection within the patches, adults come together to form a single mating pool. Can the P allele invade?
|
| **iii) |
The PP homozygote has fitness 0.8 times that of QQ in environment A and 2.1 times that of QQ in B. What will eventually happen in cases i) and ii) if allele Q is introduced at low frequency?
|
|
Problem 17.8
A population of butterflies is polymorphic for two different wing patterns. One is cryptic; the other is conspicuous and mimics a model species that is distasteful to birds. The species in question is palatable to birds, and so this is an example of Batesian mimicry (see p. 506). The polymorphism is maintained by negative frequency-dependent selection: As the mimetic pattern becomes more common in the palatable species, birds will be less likely to associate that pattern with distastefulness, and so will eat it more often.
The polymorphism depends on two alleles at a single autosomal locus; the homozygote for one allele (say, PP) is mimetic, and the other two genotypes (QP and QQ) are cryptic. Butterflies with the cryptic pattern have a 60% chance of surviving to reproduce, and mimetic butterflies have a chance 1 – 0.9u of surviving, where u is the frequency of the conspicuous pattern. Thus, if hardly any butterflies carrying that pattern are palatable (u = 0), then they gain complete protection from predation, whereas if all the palatable butterflies have the conspicuous pattern (u = 1), they lose almost all protection and only 10% survive.
|
| *i) |
At equilibrium, what is the frequency of the conspicuous pattern? What is the frequency of the allele that determines it? HINT 17I
|
| **ii) |
How quickly will the conspicuous pattern increase from a frequency of 1%? How quickly will it decrease from a frequency of 99%? HINT 17J
|
| **iii) |
What is the average fitness of the population at equilibrium? Sketch a graph of the mean fitness against allele frequency. Does the population evolve to maximum fitness? HINT 17K
|
|
Problem 17.9 *C28*
A recessive allele, P, increases fitness by s; that is, the fitnesses of genotypes QQ, PQ, PP are 1, 1, 1 + s.
|
| **i) |
Write the exact formula for the change in allele frequency, Δp, from one generation to the next. HINT 17L
|
| **ii) |
Approximate this by a differential equation that describes how allele frequency changes continuously through time. HINT 17M
|
| ***iii) |
By thinking of elapsed time as a function of allele frequency, integrate this differential equation. HINT 17N
|
| ***iv) |
Assuming a selection coefficient s = 1%, how long will it take for this recessive allele to increase from a frequency of 0.01 to 0.99? How long will it take to increase from 0.0001 to 0.99?
|
| **v) |
How do these times compare with the times taken for an allele with an additive effect to increase? Assume the same total effect of substituting P for Q, so that the genotypes QQ, PQ, PP now have fitnesses 1, 1.005, 1.01.
|
| **vi) |
Suppose now that the recessive allele gave a slight advantage in the heterozygote, so that fitnesses are 1, 1.001, 1.01. How will this alter the time taken to increase from 0.0001 to 0.99? (A qualitative answer will be enough here.)
|
|
Problem 17.10
A species with a predominantly haploid life cycle is split into two separate populations. The initial genotype at genes A, B is AQBQ; these two genes are unlinked. In one population, an allele AP arises, with selective advantage s = 10%. In the other, an allele BP with the same selective advantage arises at the other gene. These two alleles are incompatible with each other: Genotypes APBP die. Therefore, the two populations have become partially reproductively isolated. We discuss this mechanism of speciation further in Chapter 22 (see pp. 642–644).
|
| **i) |
A hybrid population forms, as a mixture between the divergent populations. What is the mean fitness of a population with allele frequencies pA, pB? Sketch the adaptive landscape by plotting contours of mean fitness against allele frequencies. HINT 17O
|
| **ii) |
Find the general expression for the average fitnesses of alleles AQ, AP, and so find the change in allele frequency, ΔpA, from one generation to the next after admixture.
|
| **iii) |
*C28* Show that this change is proportional to the gradient of the adaptive landscape (d /dpA). HINT 17P
|
|
Problem 17.11
The increase in mean of a quantitative trait caused by a selection gradient β is R = VAβ, where VA is the additive genetic variance (p. 478). The selection gradient is defined as the slope of the relationship between fitness and trait value, divided by the mean fitness (i.e., individual fitness can be written as approximately W = (1 + β (z – 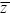 )), where z is the value of the trait in an individual and W is the individual’s fitness, which depends on z). In this problem, we show how this description at the level of the phenotype is related to selection on individual alleles.
|
| *i) |
Suppose that each copy of an allele adds α to the trait value; the frequency of the allele is p. How much does the trait mean increase when allele frequency increases by Δp? (Assume that the organism is diploid.)
|
| **ii) |
With a selection gradient β, what is the rate of increase of allele frequency? Hence, find the rate of change of the mean due to this allele. HINT 17Q
|
| **iii) |
Show that this is equal to β times the additive variance contributed by the allele.
|
|
Problem 17.12
|
| *i) |
Additive genetic variance in a quantitative trait is generated by mutation at a rate Vm = 0.002VE and is lost by random drift; the effective population size is Ne = 250. There are a large number of mutations of individually small effect. What is the heritability of the trait at an equilibrium between mutation and random drift?
|
| **ii) |
The trait is under steady artificial selection, with selection differential S = 0.4 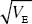 . NOTE 17C What is the rate of increase of the trait mean when genetic variance is at a mutation-drift equilibrium? Assume that selection does not alter the variance of the trait. NOTE 17D
|
| **iii) |
Suppose that an allele with relatively large effect, α = 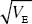, arises. What is the selection coefficient favoring it? (The selection differential stays the same as in i).)
|
| ***iv) |
Draw graphs showing the pattern of change in the trait mean and the transient increase in genetic variance that it contributes. Would the presence of this allele be detectable from such observations? HINT 17R HINT 17S
|
| **v) |
Now, suppose that the allele is a recessive lethal. What will its frequency be at equilibrium? What trait variance will it contribute at equilibrium?
|
