The Hawk–Dove Game

When a range of possible invading strategies have the same fitness when played against the resident, an additional criterion is used to determine the ESS. Once the invader has reached an appreciable frequency, both invaders and residents will meet invaders. Given that invaders and residents have exactly the same payoff when they meet residents, the outcome is now determined by the outcome of contests with the invaders. We must ask what happens when the invader meets itself, compared with what happens when a resident meets the invader.

An invader plays hawk with probability P and dove with probability 1 – P; and the residents play hawk and dove with equal probability. So, the four possible outcomes when a resident meets an invader have probabilities

Multiplying these by the payoffs for each of the four cases (Box 20.4c), we find that when a resident meets an invader, it wins

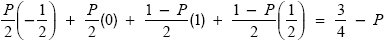
on average. A similar calculation shows that when an invader meets another invader, it wins

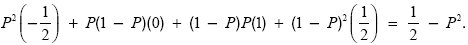
Because this is never greater than the payoff to a resident, no strategy can invade: The resident strategy P = 1/2 is therefore an ESS.

Figure WN20.7 summarizes these arguments. When the population is playing a mixed strategy, such that each individual plays hawk half the time and dove the other half, then any strategy has the same expected payoff (1/4) when played against a resident (horizontal line). Now, a strategy can invade only if an invader playing against an invader gets a higher payoff than a resident playing against an invader. In this example, no strategy can meet this condition, so that playing P = 1/2 is indeed an ESS.