The Probability of Fixation of a Slightly Advantageous Allele

Assume that the favorable alleles have a slight selective advantage (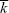 = 1 + s, where s << 1). Then, the fixation probability does not depend on the (usually unknown) shape of the distribution of offspring number, f_k, but instead only depends on its variance. It is easiest to work in terms of the probability of ultimate survival, P = 1 – Q, because this will be small when s is small. We approximate Q^k = (1 – P)^k as 1 – kP + [k(k – 1)/2] P², ..., giving

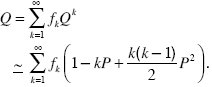
Now,

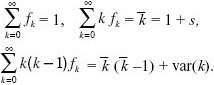
Because we are assuming that 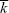is close to 1, this last term can be further approximated to var(k), the variance in offspring number. Thus,

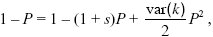
so that

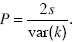
We consider the simplest case where genes or individuals have a single growth rate. Branching processes also describe situations where genes can be found in different places, or associated with different genes at other loci, provided they reproduce independently of each other. One such example is worked through here, based on the deterministic model of Box 28.3. For a comprehensive textbook on branching processes, see Harris (1963), and for an application to evolutionary problems, Barton (1995) and Otto and Day (2007, Chapter of 14.5).