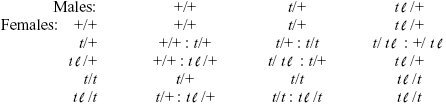
NOTE 21E: A full calculation of the dynamics is complicated, because there will be some association (i.e., some linkage disequilibrium) between the restorer allele and the sterility allele, although this will be weak, because the genes are not linked. There may be a polymorphism if the restorer allele has some cost; in addition, the sterility allele gains some extra advantage by avoiding self-fertilization and hence inbreeding depression. On the other hand, selfing by male-fertile plants may prevent the population becoming extinct. Finally, new restorer alleles and new sterility alleles may evolve, so that there will be a continuing coevolution between these genes. This “arms race” is ultimately caused by a conflict between genes that are inherited in different ways. See Web Notes.
NOTE 21F: It is not known exactly how Wolbachia spreads through California, although detailed estimates of the various effects on fitness have been made. See Turelli and Hoffman (1995).
NOTE 21G: The upper equilibrium is in fact not stable; growth rates are so high that numbers fluctuate chaotically between low and high values. Nevertheless, the population persists, barring chance extinctions.
NOTE 21H: The argument is complicated by chaotic fluctuations of N around the (unstable) equilibrium, but the conclusion in fact is identical to that given by the naive argument.
NOTE 21I: This situation is similar to that with male sterility in plants; recall Problem 21.2.
NOTE 21J: The full problem is quite complicated: We have five viable genotypes, although only three male genotypes are fertile. We can find the progeny from each of the 15 possible fertile matings:
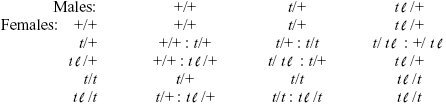
We could write down equations for the change of the five genotype frequencies through time. However, it is simplest to think about the extreme cases, as in the answers here.
NOTE 21K: In a growing population, there will be more siblings, and so a greater relative advantage. In addition, strong selection will itself distort relationships, and so the r in this calculation is a slight approximation. See Web Notes.
NOTE 21L: This could also be determined by finding the probability of identity by descent between two X-linked genes in siblings.
NOTE 21M: We ignore inbreeding depression here, which might reduce this extra contribution.
NOTE 21N: Many plant species have evolved mechanisms for selective seed abortion, see Web Notes.
NOTE 21O: Recall several examples where behaviors caused by a “selfish” gene can cause severe fitness loss in relatives (e.g., Fig. 21.7).
NOTE 21P: We often talk of the optimal allocation “from the point of view” of a gene. Strictly speaking, we should consider whether an allele that has some effect on resource allocation would increase in the population. What matters is where the allele has its effect: on how the parent plant allocates resources or on how an individual embryo can influence the amount of resource that it gets. This problem shows how alleles that are expressed in different contexts will cause different resource allocations to evolve. The outcome therefore depends on what kind of alleles can influence allocation. In this example, it is most likely to be alleles expressed in the mother.
NOTE 21Q: We have ignored complications such as the delay, ~(1/s)log(N) generations between establishment and fixation, by assuming that almost all demes are near fixation for one or other allele.
NOTE 21R: With higher migration rates (Nm ~1, say), group selection becomes much less effective relative to individual selection. The rate of increase due to individual selection depends on the effective selection coefficient, ~s(1 – FST), and the response to selection on extinction rate is ~(λQ – λP)FST. As FST gets smaller, the balance between individual and group selection shifts.