Genetic Variability under the Infinite-Alleles Model

Once we know the shape of the genealogy that relates the genes in a sample, it is easy to work out the pattern of mutation that would be seen. Under the infinite-sites model, in which every mutation occurs at a new site, the average number of differences between two genes is 4N_eµ (see p. 426, top). Using the infinite-alleles model, we can only ask whether or not two genes carry the same allele or different alleles. Here, we show how the probability that two genes are in the same allelic state (i.e., the homozygosity, denoted F) can be found.

Two genes can share the same allelic state only if there have been no mutations since they shared a common ancestor. If that ancestor lived t generations back, then the two lineages span 2t generations, and the chance that there have been no mutations is (1 – µ)^2t ~ exp(–2µt). Now, we know that the distribution of coalescence time, ψ(t), is exponential, with mean 2N_e generations (i.e., ψ(t) = 1/2N_e)exp(–t/2N_e); see Properties of the Colescent Process and Table 28.1). Averaging over this distribution,

The chance that two randomly chosen genes carry different alleles (i.e., the gene diversity) is H = 1 – F = 4N_eµ/(1 + 4N_eµ).

We can get to the same result by following two genes from one generation back to the previous generation. For these genes to be in the same state, there must have been no mutations to either gene; the chance of this is (1 – µ)². There is a chance 1/(2N_e) that they descend from the same ancestral gene in the previous generation. If they did not, then the probability that they were identical in state was just F. Putting all this together, we can relate the homozygosity now to the homozygosity one generation back:

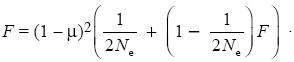
Assuming that mutation and drift are slow (µ << 1, N_e >> 1), the solution to this equation gives the same result as before. Either of these two methods can be extended to make predictions for more complicated models of mutation or population structure.