Balancing Selection in a Heterogeneous Environment: The Levene Model

When do heterogeneous selection pressures lead to a frequency-dependent selection that maintains genetic variation? The simple model described here shows that different genotypes must exploit different resources.

Suppose that an insect can lay its eggs on two different kinds of host plants, call them A, B. For simplicity, we will assume that half the eggs are laid on A and half on B, but the argument is the same for other proportions. Correspondingly, there are two types of insect in the population, each best adapted to one of these hosts. Their frequencies are p_a, p_b (p_a + p_b = 1). These two types could be determined by a single locus with two alleles, one dominant over the other. However, the genetics are not important for the argument.

The outcome depends on the survival of each type on each host plant. We write the viability of type a on plant B as V_aB, and similarly for the other three combinations:

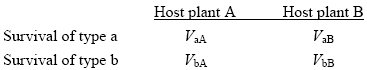
First, suppose that the numbers of larvae that successfully emerge from each plant are simply proportional to the numbers that survive on that plant. This is known as hard selection. Then, the total number of each type in the adult population is just the sum of the contributions from each kind of host:

If variation is to be maintained, then both types must be able to increase from low frequency. In other words, the polymorphism must be protected). But that is impossible, because the survival of a, averaged over both hosts, is either better than that of b ((1/2)(V_aA + V_aB) > (1/2)(V_bA + V_bB)), in which case it will win, or it is worse, in which case it will be lost.

However, variation can be maintained if the numbers of larvae emerging from each host plant are fixed, because of strong competition between larvae for the limited resource offered by the host plant. This is known as soft selection in which the numbers produced from each patch are independent of genotype frequencies. Suppose that each type of host plant contributes half of the adults:

These formulae simplify if we concentrate on what happens when either type is rare. When p_a << 1, the proportion of this type among adults is

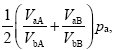
because we can set p_a = 0, p_b = 1 in the denominators at top right. So, type a will increase if

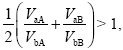
and similarly, type b will increase if

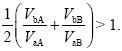
These conditions can easily be satisfied if each genotype has a large advantage on one host and a large disadvantage on the other. For example, if V_aA = 2V_bA, and V_bB = 3V_aB, both types increase when rare.

Figure 18.22B summarizes these conditions for polymorphism. The two axes show the survival of type a, relative to type b, on the two kinds of host, and the shaded area shows conditions that allow polymorphism. Crucially, it is very difficult to maintain polymorphism by this mechanism when selection is weak (i.e., when the survival rates of the two types are similar, near the point where the two curves touch at (1,1)). This makes it implausible as a general mechanism for the maintenance of variation.

Polymorphism is much easier if the types choose to exploit different hosts. Figure 18.22C shows the conditions for polymorphism when 75% of type a start out on host A, and similarly for type b on host B. Now, polymorphism is possible for a wide range of viabilities (shaded area). Indeed, polymorphism can be maintained even if there are no survival differences (cross at (1,1), or if the types prefer hosts to which they are worse adapted (region below and right of cross). What maintains polymorphism in this and other models is the exploitation of different resources: Rare types do better just because they suffer less competition within their preferred niche.

This model was first proposed by Levene in 1953, and the importance of habitat preference was explained by Maynard Smith in 1966. For more detail, see Maynard Smith and Hoekstra (1980) and Hoekstra et al. (1985).