Chapter 18 Notes
The Interaction between Selection and Other Forces
Selection and Random Drift
Most New Mutations Are Lost by Chance, Even if They Increase Fitness
The formula stating that fixation probability is about 2s is an approximation that is accurate for selection coefficients less than about 10% (Chapter 28).
Recall that on pages 407–408, we set out Fisher’s geometrical argument that mutations of small effect are most likely to contribute to complex adaptations, because they are less likely to disrupt finely tuned functions. In this section, we have seen that the chance that a mutation is actually picked up by selection is proportional to its effect on fitness. Allowing for the greater chance of fixation of mutations with larger effects increases the typical size of mutations that contribute to adaptation. Nevertheless, Fisher’s argument still implies that the mutations that build up complex adaptations will tend to have smaller effects than those contributing to simpler functions. For more detail, see Orr (1998, 2000).
In this section, we have looked at the probability that individual favorable alleles will fix. Robertson (1960) used this theory to show that , summed over generations, is just R = 2NeR1, where R1 is the response in the first generation (see p. 478). The key assumption is that the initial standing variation is lost mainly by random drift. The response at 50 generations can be predicted in a similar way, assuming the infinitesimal model, and fits the data surprisingly well.
Populations Diverge Because They Pick Up Different Favorable Mutations
Wallin et al. (2001) show that warfarin resistance (or, at least, one form of it) is due to changes in a chaperone protein that binds to vitamin K oxide reductase, not changes in the enzyme itself. However, this does not alter our argument.
Drummond (1966) describes the spread of resistance. Greaves et al. (1977) give evidence for heterozygote advantage. Greaves et al. (1982) show that different alleles are responsible for resistance in different areas. Kohn et al. (2000, 2003) give evidence for selection on the warfarin resistance gene, based on distorted patterns of variation at linked marker loci (see pp. 536–538).
Figure 18.4 is from Vogel and Motulsky (1997) and Weatherall (2001). Weatherall (2001) discusses the heterogeneity of genetic resistance to malaria, and Weatherall (2004) gives a fascinating history of research on β-thalassemias.
Jenkins et al. (2001) show how random drift is important even in very large viral populations.
Cooper et al. (2001) show by constructing artificial deletions that the advantage of deletions in the ribose operon is directly due to the deletion rather than to some other genetic change. As we saw on pp. 405–407, this is a key test for the identification of the causal genetic variant.
The example of Figure 18.5 is from Lenski and Travisano (1994), Cooper and Lenski (2000), and Cooper et al. (2001).
In Small Populations, Deleterious Alleles Can Be Fixed by Chance
The formula for fixation probability is discussed by Kimura (1983, Chapter 3).
Kondrashov (1995) lays out the argument of Box 18.1, that chance fixation of weakly deleterious mutations can substantially degrade fitness.
Figure 18.6 shows a range of selection coefficients, of magniude less than about s ~ 1/Ne, which are effectively neutral. Tomoko Ohta developed a version of the neutral theory that allows for the fact that in a large population, a smaller fraction of mutations will be effectively neutral. For reviews, see Ohta (1996, 2002) and Ohta and Gillespie (1996).
The values that go into the rough calculation in Box 18.1 are justified as follows. We assume a mutation rate for humans of 2.5 × 10–8 per generation or 175 per diploid genome (Nachman and Crowell 2000), based on rates of pseudogene divergence. We assume 35,000 genes each of length 1500 bp, but count two-thirds of the sites as liable to change amino acid sequence, giving an average target of 1000 bp. This gives a total mutation rate of 35,000 × 1,000 × 0.000000025 = 0.9 per haploid genome per generation. We then take Ne as π/(4µ) = 0.0008/(4 × 0.000000025) = 8000. Lynch et al. (1999) give a simpler calculation, which just assumes that selection has been relaxed entirely and calculates the total rate of decline due to mildly deleterious alleles at 4% per generation—a very much higher figure. Our calculation is pessimistic, because many previously deleterious mutations may now be more or less neutral. (Note that the number of genes in the human genome assumed here is too low: Current estimates are around 25,000. However, it is also clear that much noncoding DNA is selected [pp. 542–547]. Overall, therefore, our estimate of the rate of decline due to fixation of mildly deleterious mutations is probably too low.)
The balance between mutation, selection, and random drift can be understood by considering (see also Problem 18.2).
Populations Cluster around Peaks on Wright’s Adaptive Landscape
Provine (1986) reviews Wright’s derivation and use of his formula, Equation 18.1 (p. 495). Although remarkably general, this formula does neglect linkage disequilibrium and recombination, it does not allow for frequency-dependent fitnesses, and it requires special kinds of migration and mutation. Crow and Kimura (1970) discuss the mathematics of the formula.
The rate of shifts between adaptive peaks was first calculated by Wright (1941); later papers include Lande (1985) and Barton and Rouhani (1987).
Selection and Gene Flow
Favorable Alleles Spread Rapidly, Even if the Population Is Subdivided
Note that the Cooper et al. (2001) calculation of the time taken to get a deletion to 50% is not quite right as published; they use logarithms to base 2 instead of natural logs to base e.
Note that σ2 is the variance of distance moved in a generation, which has units (distance)2 per generation; σ is the typical distance moved in one generation along a given direction (p. 442).
Shigesada and Kawasaki (1997) review biological invasions, in which a species spreads into a new habitat. This process is also described by Fisher’s equation for a wave of advance.
When a new allele (or a new species) invades, the numbers of copies at the leading edge may be very small. Thus, there can be considerable random drift, even if the equilibrium population density is high. This phenomenon, known as “genetical surfing,” has received much attention recently (e.g., Edmonds et al 2004; Klopfstein et al. 2006; Ackland et al. 2007). Hallatschek et al. (2007) give a nice empirical example, in the spread of a bacterial population across a Petri dish.
The Spread of Replicating RNA Molecules Can Be Studied in the Laboratory
Figure 18.11 is from McCaskill and Bauer (1993). See also Bauer et al. (1989) and McCaskill (1997).
McCaskill and Bauer’s (1993) prediction for wave speed is slightly different from that given here. They cite a radius of a globular protein of similar molecular weight to the enzyme-RNA complex as 4.9 nm, rather than the 4.2 nm inferred from observed wave speed. Turning that round, the observed diffusion rate calculated from the Stokes equation is D = (4.2/4.9) (0.4 × 10–10) m2 s–1 = 3.43 × 10–11 m2 s–1. The growth rate is 0.013 s–1 and so Fisher’s equation gives 2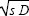 = 1.34 × 10–6 compared with 1.45 × 10–6, which are in good agreement. (Note that in physics, the diffusion coefficient is defined as D = σ2/2.) = 1.34 × 10–6 compared with 1.45 × 10–6, which are in good agreement. (Note that in physics, the diffusion coefficient is defined as D = σ2/2.)
Even if no RNA is added, monomers will aggregate spontaneously to produce some random sequence. This sequence is then selected to replicate rapidly, so that the sequence which emerges has the highest fitness under the experimental conditions. In one example of such a de novo origin of genetic information, several sequences emerged spontaneously, and each spread out at a steady rate. The speed of the wavefront indicates the rate of replication (i.e., the fitness). , one variant was established early on and was replaced by a slightly fitter variant as it spread and eventually replaced other variants that had been spreading more slowly.
Geographic Patterns (Clines) Can Be Produced in a Variety of Ways
Figure 18.12 is from Nachman et al. (2003). Haldane’s (1948) original mathematical analysis of clines was stimulated by Sumner’s (1932) and Dice and Blossom’s (1937) data on this system.
Barton and Hewitt (1985) review how alternative explanations for clines can be distinguished.
Figure 18.13B,C is from Christiansen (1977).
Another example of a cline that spans a broad geographic scale, and so is likely to be maintained by selection alone, is the polymorphism for . This polymorphism is controlled by two genes, one of which produces a precursor glucoside and the other of which codes for an enzyme that breaks down the glucoside when tissues are damaged. The pies show the frequency of the allele that generates the precursor glucoside; allele frequencies at the other locus are similar (from Daday 1954; see also Ennos 1982).
Narrow Clines Can Be Maintained by a Balance between Selection and Gene Flow
Figure 18.14B is redrawn from McNeilly (1968).
Figure 18.15 is from Lenormand et al. (1999).
Details of the hybrid zone in Podisma pedestris (Fig. 18.16) are in Barton and Hewitt (1989).
Figure 18.17 is from Mallet and Barton (1989).
Cline Width Is Proportional to a Characteristic Scale Set by the Relative Rates of Dispersal and Selection
Equations that combine a diffusion term with the effect of other processes, such as selection, are known as reaction-diffusion equations. They were introduced to population genetics by Fisher (1937, 1950) and Haldane (1948) and have the same form as those used by Turing (1952) to explain the patterns that arise in development as a result of diffusible morphogens. The theory of clines was revived by Slatkin (1973) and May et al. (1975) and by a series of papers by Nagylaki (e.g., 1975). Endler (1977), Felsenstein (1976), and Roughgarden (1979) review this literature. See Chapter 28.
In the Podisma calculation, we ignore the small adjustment that is needed to account for the fact that this chromosome rearrangement is sex-linked. Because only two-thirds of X chromosomes is in females, the average selection coefficient is two-thirds of that in females.
We summarize the widths of different kinds of clines, relative to the characteristic scale .
Balancing Selection
Heterozygote Advantage Is Unlikely to Be the Main Form of Balancing Selection
Allozyme studies of haploid and inbreeding organisms include Spieth (1975) and Marshall and Allard (1970). Charlesworth and Charlesworth (1995) and Hamrick and Godt (1996) review the effects of inbreeding on quantitative genetic variation in plants.
If heterozygote advantage were a common cause of genetic diversity in outcrossing diploids, then other puzzles arise. Gene duplications could fix both alleles in one genome, so that the segregation of less-fit homozygotes would be avoided. For example, rats carrying a duplication with both resistant and sensitive alleles of the warfarin resistance gene would be able to synthesize the vitamin in the presence of the poison and would also carry the more efficient wild-type allele. A population fixed for such a duplication would avoid the production of unfit homozygotes that were either sensitive to warfarin or suffered vitamin K deficiency. As another example, and more fundamentally, widespread heterozygote advantage would favor asexual reproduction, which could allow the fit heterozygotes to avoid the costs of sex. We examine these issues further in Chapter 23.
Genetic Variation Can Be Maintained If Selection Favors Rare Alleles
The Oenothera organensis example (Fig. 18.18) comes from Emerson, as cited in Provine (1986). This case fueled the argument between Fisher and Wright over how diversity could be maintained despite drift in small populations (Provine 1986). The modern molecular work on species such as Physalis mostly does not test for the functional allelic classes—the DNA sequence alone does not show which alleles will be incompatible with which. Hence, this Oenothera example is still one of the best.
Figure 18.19 is from Lu (2002).
Edwards (1998, 2000) discusses the history of the argument that the sex ratio is kept even by frequency-dependent selection. It was given by Darwin (1871) in the first edition of his Descent of Man, and selection in relation to sex, but dropped from later editions. Carl Dusing published a mathematical analysis in 1884. However, Fisher did not give any prior references in his 1930 book, so that the argument is now associated with his name.
Ford (1964) discusses the Papilio example (Fig. 18.20), although with sparse field data. Numbers are given for one sample from Nairobi that shows high polymorphism.
Figure 18.21 is from Rainey and Travisano (1998).
Only Certain Kinds of Fluctuating Selection Can Maintain Variation
The model illustrated in Figure 18.22 was first used by Levene (1953). It is used to show how selection acts on recombination in Figure 23.13. This Levene model is explained in more detail .
Coevolution May Be an Important Source of Variation
Interactions between host and parasite can maintain variation, because rare host genotypes tend to be less heavily parasitized and because hosts tend not to be immune to new parasite genotypes while those remain rare. However, there is no direct dependence of fitnesses on the frequencies of genotypes within the same species. So, one would not usually call such interactions “frequency-dependent selection.”
Haldane and Jayakar (1963) developed the theory for fluctuating selection; see also Felsenstein’s (1976) review. Haldane (1949) drew attention to the importance of disease in driving evolutionary change. W.D. Hamilton made the case in a series of papers, paying particular attention to the consequences for sexual selection (Chapter 20) and for the evolution of sex (Chapter 23). These papers are collected in Hamilton (1996), accompanied by idiosyncratic commentaries.
Figure 18.23 is from Bell (1997).
Figure 18.24 is from Dybdahl and Lively (1998) and Lively and Dybdahl (2000).
Mutation and Selection
Deleterious Mutations Are Responsible for Much Variation
Kondrashov (1988) is an influential review, which stimulated much of the recent interest in the importance of deleterious mutations. See also Lynch et al. (1999).
Danforth (1921) first showed how mutation and selection on dominant alleles in humans could be estimated. Haldane (1935) rediscovered this independently. See Vogel and Motulsky (1997, Chapter 9).
Table 18.1 is from Vogel and Motulsky (1997, Table 9.8).
Figure 18.25 is from Jenkins et al. (2001).
The original argument, made by Wright et al. (1942), that recessive lethals are mainly eliminated by selection against heterozygotes is explained . Lewontin et al. (1981) provide an interesting commentary.
Mutation Maintains Variation in Quantitative Traits
A recent experiment by Weber et al. (2005) gives evidence of extensive pleiotropy. They found that 11 of 50 random insertions of transposable elements had significant effects on wing shape. None of these insertions was near candidate genes. This suggests that about one-fifth of all genes affects this one trait.
Kimura (1965) and Lande (1975) set out models in which mutation maintains a “continuum of alleles” at each locus, that is, a large number of alleles each with small effects, which give an approximately normal distribution of effects of each locus. Turelli (1984) argued that these models require unrealistically high mutation rates per locus and that with more realistic parameters, each locus will typically have one common wild-type allele, with rare variants of relatively large effect. Mutation then cannot easily maintain high heritabilities. Turelli (1985) and Wagner (1989) further argued that pleiotropy makes mutation still less likely as an explanation. We summarize these later analyses , making the simplifying assumption that there are just two alleles per locus. Burger (2000) reviews these mathematical models.
Variation in Quantitative Traits May Be a Side Effect of Polymorphisms Maintained for Other Reasons
See Barton (1990) and Barton and Keightley (2002).
Inbred Individuals Are Less Fit: Inbreeding Depression
The Mandarte Island example is from Marr et al. (2002); for a review of inbreeding effects in the wild, see Keller and Waller (2002).
Figure 18.27 is from Coltman et al. (1999).
Figure 18.28B,C is from Saccheri et al. (1998).
For a review of measurements of inbreeding depression in humans, see Vogel and Motulsky (1997, Chapter 13).
Goudet and Keller (2002), Slate et al. (2004), and Hansson and Westerberg (2008) give recent reviews of correlations between marker heterozygosity and fitness.
We discuss the population genetic implications of small population size , especially with respect to conservation of endangered species.
Inbreeding Depression Can Be Caused by Deleterious Recessive Mutations or by Overdominance
Figure 18.30 is from a survey of 28 studies by Crnokrak and Barrett (2002).
References
Ackland G.J., Signitzer M., Stratford, K., and Cohen M.H. 2007. Cultural hitchhiking on the wave of advance of beneficial technologies. Proc. Natl. Acad. Sci. 104: 8714–8719.
Adams M.D., Celniker S.E., Holt R.A., et al. 2000. The genome sequence of Drosophila melanogaster. Science 287: 2185–2195.
Barton N.H. 1990. Pleiotropic models of quantitative variation. Genetics 124: 773–782.
Barton N.H. and Hewitt G.M. 1981. A chromosomal cline in the grasshopper Podisma pedestris. Evolution 35: 1008–1018.
Barton N.H. and Hewitt G.M. 1985. Analysis of hybrid zones. Annu. Rev. Ecol. Syst. 16: 113–148.
Barton N.H. and Hewitt G.M. 1989. Adaptation, speciation and hybrid zones. Nature 341: 497–503.
Barton N.H. and Keightley P.D. 2002. Understanding quantitative genetic variation. Nat. Rev. Genet. 3: 11–21.
Barton N.H. and Rouhani S. 1987. The frequency of shifts between alternative equilibria. J. Theor. Biol. 125: 397–418.
Bauer G.J., McCaskill J.S., and Otten H. 1989. Travelling waves of in vitro evolving RNA. Proc. Natl. Acad. Sci. 86: 7937–7941.
Bell G. 1997. Selection: The mechanism of evolution. Chapman and Hall, New York.
Burger R. 2000. The mathematical theory of selection, recombination and mutation. Wiley, Chichester.
Charlesworth D. and Charlesworth B. 1995. Quantitative genetics in plants: The effect of the breeding system on genetic variability. Evolution 49: 911–920.
Christiansen F.B. 1977. Population genetics of Zoarces viviparus. In Lecture notes in biomathematics: Measuring selecvtion in natural populations (ed. F.B. Christiansen and T.M. Fenchel), pp. 21–48. Springer-Verlag, Berlin.
Coltman D.W., Pilkington J.G., Smith J.A., and Pemberton J.M. 1999. Parasite-mediated selection against inbred Soay sheep in a free-living, island population. Evolution 53: 1259–1267.
Cooper V.S. and Lenski R.E. 2000. The population genetics of ecological specialization in evolving Escherichia coli populations. Nature 407: 736–739.
Cooper V.S., Schneider D., Blot M., and Lenski R.E. 2001. Mechanisms causing rapid and parallel losses of ribose catabolism in evolving populations of Escherichia coli B. J. Bacteriol. 183: 2834–2841.
Crnokrak P. and Barrett S.C. 2002. Purging the genetic load: A review of the experimental evidence. Evolution 56: 2347–2358.
Crow J.F. and Kimura M. 1970. An introduction to population genetics theory. Harper & Row, New York.
Daday H. 1954. Gene frequencies in wild populations of Trifolium refens L. I. Distribution by latitude. Heredity 8: 61–78.
Danforth G.H. 1921. The frequency of mutation and the incidence of hereditary traits in man. In Eugenics, genetics and the family, vol. I., pp. 120–128. Scientific papers of the Second International Congress of Eugenics held at the American Museum of Natural History, New York, September 22–28, 1921 (Charles B. Davenport, Chairman, H.H. Laughlin, Secretary, committee on publication). Williams and Wilkins Company, Baltimore, 1923.
Darwin C. 1871. The descent of man, and selection in relation to sex. John Murray, London.
Dice L.R. and Blossom P.M. 1937. Studies of mammalian ecology in southwestern North America, with special attention to the colors of desert mammals. Carnegie Inst. Wash. Publ. 485: 1–129.
Drummond D. 1966. Rats resistant to warfarin. New Sci. 30: 771–772.
Düsing C. 1884. Die Regulierung des Geschlechtsverhanisses. J. Natwiss. 17: 593–940.
Dybdahl M.F. and Lively C.M. 1998. Host–parasite coevolution: Evidence for rare advantage and time-lagged selection in a natural population. Evolution 52: 1057–1066.
Edmonds C., Lillie A.S., and Cavalli-Sforza L.L. 2004. Mutations arising in the wave front of an expanding population. Proc. Natl. Acad. Sci. 101: 975–979.
Edwards A.W.F. 1998. Natural selection and the sex ratio: Fisher’s sources. Am. Nat. 151: 564–569.
Edwards A.W.F. 2000. Carl Düsing (1884) on the regulation of the sex-ratio. Theor. Popul. Biol. 58: 255–257.
Endler J.A. 1977. Geographic variation, speciation, and clines. Princeton University Press, Princeton, New Jersey.
Ennos R.A. 1982. Association of the cyanogenic loci in white clover. Genet. Res. 40: 65–72.
Felsenstein J. 1976. The theoretical population genetics of variable selection and migration. Annu. Rev. Genet. 10: 253–280.
Fisher R.A. 1930. The genetical theory of natural selection. Oxford University Press, Oxford.
Fisher R.A. 1937. The wave of advance of advantageous genes. Ann. Eugenics 7: 355–369.
Fisher R.A. 1950. Gene frequencies in a cline determined by selection and diffusion. Biometrics 6: 353–361.
Ford E.B. 1964. Ecological genetics. Methuen, London.
Goudet J. and Keller L. 2002. The correlation between inbreeding and fitness: Does allele size matter? Trends Ecol. Evol. 17: 201–202.
Greaves J.H. and Ayres P.B. 1982. Multiple allelism at the locus controlling warfarin resistance in the Norway rat. Genet. Res. 40: 59–64.
Greaves J.H., Redfern R., Ayres P.B., and Gill J.E. 1977. Warfarin resistance: A balanced polymorphism in the Norway rat. Genet. Res. 30: 257–263.
Haldane J.B.S. 1935. The rate of spontaneous mutation of a human gene. J. Genet. 31: 317–326.
Haldane J.B.S. 1948. The theory of a cline. J. Genet. 48: 277–284.
Haldane J.B.S. 1949. Disease and evolution. Ricerca Scient. Suppl. 19: 68–76.
Haldane J.B.S. and Jayakar S.D. 1963. Polymorphism due to selection of varying direction. J. Genet. 58: 237–242.
Hallatschek O., Hersen P., Ramanathan S., and Nelson D.R. 2007. Genetic drift at expanding frontiers promotes gene segregation. Proc. Natl. Acad. Sci. 104: 19926–19930.
Hamilton W.D. 1996. Narrow roads of gene land, Volume 2: Evolution of sex and sexual selection. W.H. Freeman, Oxford.
Hamrick J.L. and Godt M.J.W. 1996. Effects of life history traits on genetic diversity in plant species. Philos. Trans. R Soc. Lond. B. 351: 1291–1298.
Hansson B. and Westerberg L. 2008. Heterozygosity-fitness correlations within inbreeding classes: Local or genome-wide effects? Conserv. Genet. 9: 73–83.
Hoekstra R.F., Bijlsma R., and Dolman A.J. 1985. Polymorphism from environmental heterogeneity: Models are only robust if the heterozygote is close in fitness to the favoured homozygote in each environment. Genet. Res. 45: 299–314.
Jenkins G.M., Worobey M., Woelk C.H., and Holmes E.C. 2001. Nonquasispecies evidence for the evolution of RNA viruses. Mol. Biol. Evol. 18: 987–994.
Keller L.F. and Waller D.M. 2002. Inbreeding effects in wild populations. Trends Ecol. Evol. 17: 230–241.
Kimura M. 1965. A stochastic model concerning the maintenance of genetic variability in quantitative characters. Proc. Natl. Acad. Sci. 54: 731–736.
Kimura M. 1983. The neutral theory of molecular evolution. Cambridge University Press, Cambridge.
Klopfstein S., Currat M., and Excoffier L. 2006. The fate of mutations surfing on the wave of a range expansion. Mol. Biol. Evol. 23: 482–490.
Kohn M.H., Pelz H.J., and Wayne R.K. 2000. Natural selection mapping of the warfarin-resistance gene. Proc. Natl. Acad. Sci. 97: 7911–7915.
Kohn M.H., Pelz H.J., and Wayne R.K. 2003. Locus-specific genetic differentiation at Rw among warfarin-resistant tat (Rattus norvegicus) populations. Genetics 164: 1065–1070.
Kondrashov A.S. 1988. Deleterious mutations and the evolution of sexual reproduction. Nature 336: 435–441.
Kondrashov A.S. 1995. Contamination of the genome by very slightly deleterious mutations: Why have we not died 100 times over? J. Theor. Biol. 175: 583–594.
Lande R. 1975. The maintenance of genetic variability by mutation in a polygenic character with linked loci. Genet. Res. 26: 221–236.
Lande R. 1985. Expected time for random genetic drift of a population between stable phenotypic states. Proc. Natl. Acad. Sci. 82: 7641–7645.
Lande R. 1988. Genetics and demography in biological conservation. Science 241: 1455–1459.
Lenormand T., Bourguet D., Guillemaud T., and Raymond M. 1999. Tracking the evolution of insecticide resistance in the mosquito Culex pipiens. Nature 400: 861–864.
Lenski R.E. and Travisano M. 1994. Dynamics of adaptation and diversification: A 10,000 generation selection experiment with bacterial populations. Proc. Natl. Acad. Sci. 91: 6608–6618.
Levene H. 1953. Genetic equilibrium when more than one niche is available. Am. Nat. 87: 331–333.
Lewontin R.C., Moore J.A., Provine W.B., and Wallace B. 1981. Dobzhansky’s “Genetics of natural populations” I–XLIII. Columbia University Press, New York.
Lively C.M. and Dybdahl M.F. 2000. Parasite adaptation to locally common host genotypes. Nature 405: 679–681.
Lu Y. 2002. Molecular evolution at the self-incompatibility locus of Physalis longifolia (Solanaceae). J. Mol. Evol. 54: 784–793.
Lynch M., Blanchard J., Houle D., Kibota T., Schultz S., Vassilieva L., and Willis J. 1999. Spontaneous deleterious mutation. Evolution 53: 645–663.
Mallet J.L.B. and Barton N.H. 1989. Strong natural selection in a warning color hybrid zone. Evolution 43: 421–431.
Marr A.B., Keller L.F., and Arcese P. 2002. Heterosis and outbreeding depression in descendants of natural immigrants to an inbred population of song sparrows (Melospiza melodia). Evolution 56: 131–142.
Marshall D.R. and Allard R.W. 1970. Maintenance of isozyme polymorphisms in natural populations of Avena barbata. Genetics 66: 393–399.
May R.M., Endler J.A., and McMurtrie R.E. 1975. Gene frequency clines in the presence of selection opposed by gene flow. Am. Nat. 109: 659–676.
Maynard Smith J. 1966. Sympatric speciation. Am. Nat. 100: 637–650.
Maynard Smith J. and Hoekstra R. 1980. Polymorphism in a varied environment—How robust are the models ? Genet. Res. 35: 45–57.
McCaskill J.S. 1997. Spatially resolved in vitro molecular ecology. Biophys. Chem. 66: 145–158.
McCaskill J.S. and Bauer G.J. 1993. Images of evolution: Origin of spontaneous RNA replication waves. Proc. Natl. Acad. Sci. 90: 4191–4195.
McNeilly T. 1968. Evolution in closely adjacent populations. III. Agrostis tenuis on a small copper mine. Heredity 23: 99–108.
Nachman M.W. and Crowell S.L. 2000. Estimate of the mutation rate per nucleotide in humans. Genetics 156: 297–304.
Nachman M.W., Hoekstra H.E., and D’Agostino S.L. 2003. The genetic basis of adaptive melanism in pocket mice. Proc. Natl. Acad. Sci. 100: 5268–5273.
Nagylaki T. 1975. Conditions for the existence of clines. Genetics 80: 595–615.
Ohta T. 1996. The current significance and standing of neutral and nearly neutral theories. BioEssays 18: 673–677.
Ohta T. 2002. Near-neutrality in evolution of genes and gene regulation. Proc. Natl. Acad. Sci. 99: 16134–16137.
Ohta T. and Gillespie J.H. 1996. Development of neutral and nearly-neutral theories. Theor. Popul. Biol. 49: 128–142.
Orr H.A. 1998. The population genetics of adaptation: The distribution of factors fixed during adaptive evolution. Evolution 52: 935–949.
Orr H.A. 2000. Adaptation and the cost of complexity. Evolution 54: 13–20.
Provine W. 1986. Sewall Wright and evolutionary biology. University of Chicago Press, Chicago.
Rainey P.B. and Travisano M. 1998. Adaptive radiation in a heterogeneous environment. Nature 394: 69–72.
Robertson A. 1960. A theory of limits in artificial selection. Proc. R. Soc. Lond. B 153: 234–249.
Roughgarden J. 1979. Theory of population genetics and evolutionary ecology: An introduction. Macmillan. New York.
Saccheri I., Kuusaari M., Kankare M., Vikman P., Fortelius W., and Hanski I. 1998. Inbreeding and extinction in a butterfly metapopulation. Nature 392: 491–494.
Shigesada N. and Kawasaki K. 1997. Biological invasions. Oxford University Press, Oxford.
Slate J., David P., Dodds K.G., Veenvliet B.A., Glass B.C., Borad T.E., and McEwan J.C. 2004. Understanding the relationship between the inbreeding coefficient and multilocus heterozygosity: Theoretical expectations and empirical data. Heredity 93: 255–265.
Slatkin M. 1973. Gene flow and selection in a cline. Genetics 75: 733–756.
Spieth P.T. 1975. Population genetics of allozyme variation in Neurospora intermedia. Genetics 80: 785–805.
Sumner F.B. 1932. Genetic, distributional and evolutionary studies of the subspecies of deer mice (Peromyscus). Bibl. Genetica 9: 1–106.
Turelli M. 1984. Heritable genetic variation via mutation-selection balance: Lerch’s zeta meets the abdominal bristle. Theor. Popul. Biol. 25: 138–193.
Turelli M. 1985. Effects of pleiotropy on predictions concerning mutation-selection balance for polygenic traits. Genetics 111: 165–195.
Turing A.M. 1952. On the chemical basis of morphogenesis. Philos. Trans. R. Soc. B 237: 37–72.
Vogel F. and Motulsky A.G. 1997. Human genetics: Problems and approaches. Springer-Verlag, Berlin.
Wagner G.P. 1989. Multivariate mutation-selection balance with constrained pleiotropic effects. Genetics 122: 223–234.
Wallin R., Hutson S.M., Cain D., Sweatt A., and Sane D.C. 2001. A molecular mechanism for genetic warfarin resistance in the rat. Faseb J. 15: 2542–2544.
Weatherall D.J. 2001. Phenotype-genotype relationships in monogenic disease: Lessons from the thalassemias. Nat. Rev. Genet. 2: 245–255.
Weatherall D.J. 2004. Thalassaemia: The long road from bedside to genome. Nat. Rev. Genet. 5: 1–7.
Weber K.E. and Diggins L.T. 1990. Increased selection response in larger populations. II. Selection for ethanol vapor tolerance in D. melanogaster at two population sizes. Genetics 125: 585–597.
Weber K., Johnson N.A., Champlin D., and Patty A. 2005. Many P-element insertions affect wing shape in Drosophila melanogaster. Genetics 169: 1461–1475.
Wolfe M.S. 1987. Population genetics of powdery mildew epidemics. In Populations of plant pathogens (ed. M.S. Wolfe and H. Caten), pp. 253–273. Blackwell, Oxford.
Wright S. 1941. On the probability of fixation of reciprocal translocations. Am. Nat. 75: 513–522.
Wright S., Dobzhansky T., and Hovanitz W. 1942. Genetics of natural populations. VII. The allelism of lethals in the third chromosome of Drosophila pseudoobscura. Genetics 27: 363–394.
|

