|
Problem 18.1 *C28*
A population of N haploid individuals maintains itself at steady size: Individuals produce 0, 1, or 2 offspring with probability 1/4, 1/2, 1/4, respectively.
|
| *i) |
What is the effective population size? (For a haploid population, this is defined by setting the rate of increase of variance in allele frequency to pq/Ne). HINT 18A
|
| *ii) |
A new allele arises that increases fitness: The chances of producing 0, 1, 2 offspring are now 0.24, 0.5, 0.26. Once this allele is established in many copies, how quickly does it increase? HINT 18B
|
| **iii) |
What is the probability that a single copy of the allele will eventually get fixed in the population? HINT 18C
|
| *iv) |
Show that this probability is close to the approximation 2s(Ne/N), where s is the expected rate of increase of the allele.
|
| **v) |
Plot the probability of fixation against the number of copies of the allele.
|
|
Problem 18.2
Valine is encoded by four triplet codons: GUU, GUC, GUA, and GUG (see Fig. 2.26). The mutation rate is 3 × 10–9 per site per generation, and the effective population size is Ne = 106.
|
| *i) |
Show that at a site that codes for valine, the population is likely to be close to fixation for one or other of these codons. HINT 18D
|
| *ii) |
Now, suppose that a GUU codon is more fit than the alternatives by a factor 1 + s, where s = 10–6. NOTE 18A What is the probability that a mutation from GUC to GUU will fix? What is the probability that a mutation in the opposite direction will fix? HINT 18E
|
| **iii) |
What is the frequency of GUU at equilibrium? (Assume that mutations between any pair of bases are equally frequent.) HINT 18F
|
| **iv) |
Proline is encoded by CCU, CCC, CCA, and CCG. If we observed that at sites coding for proline, CCU was the most common, at 70%, and the other three codons were all at 10%, what could we infer about the strength of selection?
|
|
Problem 18.3
Box 18.1 gives the rate of decline of fitness caused by the fixation of slightly deleterious alleles. This assumes that the effective population size is initially large, so that the fittest allele is fixed at every site, and that deleterious mutations accumulate after Ne falls to a lower size. HINT 18G
|
| *i) |
Draw a graph showing how this rate depends on the strength of selection relative to random drift, Nes.
|
| **ii) |
If population size increases, how long will it take for fitness to be restored?
|
|
Problem 18.4
A trait is under steady directional selection, with selection gradient β = 0.1/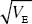 . HINT 18H Additive genetic variance is generated by mutation at a rate VM = 0.005VE and is lost by random drift; the effective population size is Ne = 100. . HINT 18H Additive genetic variance is generated by mutation at a rate VM = 0.005VE and is lost by random drift; the effective population size is Ne = 100.
|
| *i) |
What is the heritability of the trait at an equilibrium between mutation and random drift?
|
| *ii) |
What is the rate of increase of the trait mean when genetic variance is at a mutation-drift equilibrium?
|
| **iii) |
Suppose that the alleles responsible for trait variation have effect α = ±0.5 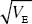 ; half have a positive effect and half have a negative effect. The mutation rate to such alleles is μ = 10–5 per diploid locus. How many loci must influence the trait in this way to account for the observed mutational variance? HINT 18I ; half have a positive effect and half have a negative effect. The mutation rate to such alleles is μ = 10–5 per diploid locus. How many loci must influence the trait in this way to account for the observed mutational variance? HINT 18I
|
| **iv) |
What is the selective advantage of each allele? What is the probability of fixation of a single copy of the favorable allele? HINT 18J
|
| **v) |
How many mutations influencing the trait enter the population in each generation? Combine these calculations to find the total rate of change of the trait mean. HINT 18K
|
|
Problem 18.5
A new allele arises by mutation, in a single copy; each copy of the allele increases fitness by 2%.
|
| *i) |
Sketch a graph showing how its frequency will increase within a single panmictic population of N = 5 × 107 diploid individuals (use a log scale). HINT 18L
|
| **ii) |
Now, suppose instead that the allele arises at the center of a population of the same total size spread over a two-dimensional range 1000 km × 1000 km and with a rate of gene flow of σ = 1 km in each generation. How will it increase and spread during the time when it is still rare? HINT 18M Approximately how long will it take for the allele to reach a frequency of 0.5 at its point of origin?
|
| **iii) |
Write down a formula for the frequency of the allele in the whole population after it has reached high frequency at its point of origin.
|
| *iv) |
Sketch a graph of the frequency in the whole population over time, including both phases. HINT 18N
|
| **v) |
How long will it take for the allele to spread through the whole population? Is most of this time spent in the first or the second phases? HINT 18O
|
|
Problem 18.6 *C28*
Two populations that are fixed for different chromosome rearrangements meet. Heterozygotes for the rearrangement have lower fertility because of problems at meiosis (see Box 12.2): Their fitness is reduced by s relative to the homozygotes, which have the same fitness.
|
| *i) |
Explain what equilibrium will be reached.
|
| **ii) |
Write down a differential equation for the rate of change in allele frequency as a result of selection against heterozygotes and gene flow through a continuous habitat, at a rate σ2. HINT 18P
|
| **iii) |
Show that p = 1/(1 + exp(–ax)) is a solution to this equation at equilibrium and find the value of the coefficient a. HINT 18Q
|
| **iv) |
How wide is the cline that separates the two chromosome rearrangements? (It is convenient to define cline width as the inverse of the maximum gradient in allele frequency; see Fig. P18.1.)
|
|
Problem 18.7 *C28*
This example explores the stability of chromosomal polymorphism in two demes, using the same methods as those in Box 28.3. A chromosomal rearrangement reduces the fertility of heterozygotes by s; homozygotes are equally fit. Two demes are initially fixed for different arrangements (Q, P, say); they exchange genes at a rate m.
|
| **i) |
Write down a pair of differential equations that give the rate of change of allele frequencies in the two demes.
|
| **ii) |
Is there an equilibrium with different arrangements common in each deme? When will this equilibrium exist? HINT 18R
|
| ***iii) |
When is this equilibrium stable? HINT 18S
This question is relevant to models of speciation, discussed on pp. 644–648: When can populations diverge so as to become partially reproductively isolated, despite gene flow?
|
|
Problem 18.8
A flowering plant reproduces as a hermaphrodite and gains equal fitness through male function (by pollinating other plants) as through female function (producing seeds that are fertilized by other plants). There is an excess of pollen, so that seeds are always fertilized, but plants compete to pollinate other flowers. The species has a gametophytic incompatibility system (see pp. 505–506), so that pollen cannot fertilize an ovule that carries an allele that is shared with the pollen. HINT 18T
|
| *i) |
Show that the population cannot survive if only two alleles are present.
|
| **ii) |
Show how genotype frequencies change from one generation to the next if three alleles are present. Plot a graph of the frequency of one of the genotypes over time, assuming that it starts at 100%.
|
| *iii) |
What equilibrium will be reached? What fraction of pollen will successfully fertilize at equilibrium? How does this alter relative fitness?
|
| **iv) |
What is the fitness advantage of a fourth allele introduced at low frequency?
|
| **v) |
What might limit the number of alleles in the population?
|
|
Problem 18.9
A haploid organism can live on two alternative habitats, A or B. Two genotypes are found, Q and P. Their survival rates on the two habitats are

|
| *i) |
First, assume that there is no competition within patches, so that the contribution to the next generation is simply proportional to the numbers that survive. (This is known as hard selection) (See Web Notes.) Will allele P increase from low frequency? Will Q increase from low frequency? Can there be stable polymorphism?
|
| *ii) |
Now, assume that each patch always makes a fixed contribution to the next generation. (After survival at the rates given above, there is such strong competition that the numbers emerging from the patch are the same, regardless of how many enter and survive early life. This is known as soft selection.) (See Web Notes.) Can the two alleles coexist if each habitat makes the same contribution to the population? HINT 18U
|
| **iii) |
Now, suppose that the contributions of habitats A, B are 1 – α, α, respectively. Over what range of α can polymorphism be maintained? HINT 18V
|
| **iv) |
Now, suppose that selection is weaker:

Over what range of α is polymorphism possible?
|
| **v) |
Finally, suppose that the alleles tend to exploit different habitats: Different genotypes of parasite might have different host preferences, for example. Allele Q is twice as likely to start in A as in B, and vice versa for P. Over what range of α is polymorphism possible for the fitnesses in the table above? HINT 18W NOTE 18B
|
|
Problem 18.10
A rare genetic disease, with incidence of 1 in 90,000 births, causes death in childhood. It is due to a recessive allele at a single gene.
|
| *i) |
If this allele is maintained by a balance between mutation and selection against homozygotes, what mutation rate would be needed to explain the data? HINT 18X
|
| **ii) |
Now, suppose that the heterozygote is slightly less fit, having a selective disadvantage of 2%. What mutation rate can you infer? HINT 18Y
|
| **iii) |
A population is somewhat inbred, with a probability of identity by descent between the two homologous genes of an individual of F = 0.05. What is the incidence of the disease in cases i) and ii)?
|
|
Problem 18.11
A quantitative trait, z, is under stabilizing selection, so that the fitness of an individual, W, declines with its deviation from the optimum, zopt:
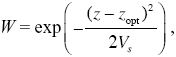
where Vs = 20VE measures the strength of selection.
|
| *i) |
What is the strength of selection against an allele with a small effect α = 0.2 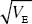 ? HINT 18Z HINT 18AA ? HINT 18Z HINT 18AA
|
| *ii) |
If there is a mutation rate μ = 10–5 to such alleles, at n = 1000 loci, what is the total mutation rate over the diploid genome, U? What is the mutational heritability, VM/VE? HINT 18BB
|
| **iii) |
What heritability is maintained at equilibrium?
|
| **iv) |
Show that VG = 2UVM, regardless of the allelic effect α or the mutation rate μ at each locus.
|
| *v) |
Now, suppose that each allele influences 20 traits, rather than one. How much genetic variance will be maintained? HINT 18CC
|
| *vi) |
If each trait influences many traits, we can combine its effects on all those traits in a single selection coefficient, 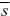 . Then, we assume that the allele has effect α on the trait in which we are interested and reduces fitness by . Then, we assume that the allele has effect α on the trait in which we are interested and reduces fitness by 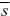 through its pleiotropic effects on other traits. If through its pleiotropic effects on other traits. If 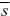 = 0.01, how much genetic variance will be maintained? = 0.01, how much genetic variance will be maintained?
|
|
Problem 18.12
Mutations to deleterious alleles occur at a rate of 10–5 at each of 10,000 genes. Each deleterious allele reduces fitness by 1% when heterozygous and by 10% when homozygous; the effects of alleles at different genes multiply together.
|
| *i) |
By how much does mutation reduce fitness at equilibrium? HINT 18DD
|
| *ii) |
What is the average fitness of an individual that is inbred, with inbreeding coefficient F? HINT 18EE
|
| **iii) |
If the population as a whole is inbred, with average inbreeding coefficient F = 0.1, how will the level of inbreeding depression change? HINT 18FF
|
| **iv) |
Now, suppose that balancing selection maintains variation at ten genes, each with two alleles; homozygotes each have fitness 10% lower than the heterozygote. How much will these genes contribute to the inbreeding depression in an outbred population? HINT 18GG HINT 18HH
|
| **v) |
Inbreeding depression may be caused by deleterious recessive mutations or by balanced polymorphisms that are maintained by heterozygote advantage (p. 516). How could you find the amount of inbreeding depression that is due to these two causes?
|

