Chapter 28 Notes
Models of Evolution
The history of modeling in evolutionary biology is explained .
There is a wide variety of for evolutionary modeling.
Mathematical Theory Can Be Used in Two Distinct Ways
Ewens (1990) contrasts these two different uses of population genetics.
Deterministic Processes
A Population Is Described by the Proportions of the Genotypes It Contains
In Figure 28.3, we give the number of diploid genotypes that can be formed when there are two alternative alleles at each of n genes as 22n. Here, we distinguish between whether genes are from the maternal or the paternal genome (so that +++/– – – is distinguished from – – –/+++). If these are equivalent, then there are 22n–1 distinct genotypes. If the genes are unlinked, so that we can count +++/– – – , +–+/– + – , ++–/– – + as equivalent, then there are only 3n distinct diploid genotypes. But, however we count, these are very large numbers.
Gradual Evolution Can Be Described by Differential Equations
In evolutionary biology, we always work with equations that give the rates of change; these are known as first-order differential equations. This contrasts with physics, where the basic equations of mechanics give the acceleration, not the velocity (i.e., d2x/dt2, a second differential of position with respect to time, not dx/dt). These equations are derived as approximations to concrete models and often approximate the behavior of a variety of different cases (discrete vs. continuous time, haploid vs. diploid, and so on).
An example that gives limit cycles is developed . This shows how the interaction between predators and their prey can lead to sustained oscillations, known as limit cycles.
Box 28.2 Solving Differential Equations
This method was first used by Haldane (1932) and is summarized in the appendix to his book, The Causes of Evolution. It is possible to write time as a function of allele frequency, t(p), for any of the usual single-locus models: selection for dominant alleles, for recessive alleles, and so on.
Populations Tend to Evolve toward Stable Equilibria
Adaptive dynamics are described by Geritz et al. (1998) and in this bibliography.
See also the critical review by Waxman and Gavrilets (2004).
Stability Is Determined by the Leading Eigenvalue
For discussion of the importance of nonlinearity, see May (1987).
Box 28.3 Migration and Selection in Two Demes
This model is analyzed by Lande (1979).
Random Processes
Our Understanding of Random Events Is Relatively Recent
Stigler (1999) and Hacking (1975) are two histories of probability.
Einstein’s (1905) paper on Brownian motion is reprinted with commentary by Stachel (1998).
Fisher (1918) introduced both analysis of variation and much of quantitative genetics. See commentary by Hill (1984).
A Random Process Is Described by Its Probability Distribution
The chi-square distribution is associated with the number of variables, n. This is referred to as the number of degrees of freedom.
Otto and Day (2007) give a comprehensive introduction to the uses of probability in biology.
Probability Can Be Thought of in Several Ways
Hacking (1965, 1975) gives thoughtful discussions of these issues, although his is only one of several points of view.
Probabilities Can Be Assigned to Unique Events
The example of Figure 28.19 is from Schär and Jendritsky (2004) and Schär et al. (2004). Also see commentary by Allen and Lord (2004).
The Increase of Independently Reproducing Individuals Is a Branching Process
Usually, we will be concerned with the fate of alleles that have a slight selective advantage (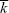 = 1 + s, where s << 1). we find a simple approximation that does not depend on the (usually unknown) shape of the distribution of offspring number, fk. = 1 + s, where s << 1). we find a simple approximation that does not depend on the (usually unknown) shape of the distribution of offspring number, fk.
The Sum of Many Independent Events Follows a Normal Distribution
The Central Limit Theorem does not apply to all distributions. Some have very fat tails (termed leptokurtic) and may have an infinitely large variance. To see this, recall that the variance is defined as the expectation of the squared deviation from the mean. If the probability declines very slowly for large values, the variance can be infinite even though the total probability mass sums to 1. One such is the Cauchy distribution, which has the form 1/(π(1 + x2)). The sum of several Cauchy variables also follows a Cauchy distribution: It does not converge to follow a Gaussian distribution, as we might expect from the Central Limit Theorem.
Box 28.6 The Diffusion Approximation
Crow and Kimura (1970) and Otto and Day (2007, Chapter 15) give simple derivations of the diffusion approximation.
The diffusion equation (Eq. 36) can only be solved if we also give the boundary conditions: What happens at the extremes, where allele frequency is p = 0 or p = 1? This is a delicate issue (see Otto and Day 2007, pp. 674–685); we give a brief outline .
Box 28.7 Selection and Migration in a Small Population
This equilibrium distribution was first derived by Wright, although without using the diffusion approximation. See Provine (1986).
References
Allen M.R. and Lord R. 2004. The blame game. Nature 432: 551–552.
Barton N.H. 1995. Linkage and the limits to natural selection. Genetics 140: 821–841.
Crow J.F. and Kimura M. 1970. An introduction to population genetics theory. Harper & Row, New York.
Düsing C. 1884. Die Regulierung des Geschlechtsverhanisses. J. Natwiss. 17: 593–940.
Edwards A.W.F. 1998. Natural selection and the sex ratio: Fisher’s sources. Am. Nat. 151: 564–569.
Edwards A.W.F. 2000. Carl Düsing (1884) on the regulation of the sex-ratio. Theor. Popul. Biol. 58: 255–257.
Einstein A. 1905. On the motion of small particles suspended in liquids at rest required by the molecular-kinetic theory of heat. Ann. Physik 17: 549–560.
Ewens W.J. 1990. Population genetics theory—The past and the future. In Mathematical and statistical developments of evolutionary theory (ed. S. Lessard), pp. 177–227. Kluwer Academic, Amsterdam.
Fisher R.A. 1918. The correlation between relatives on the supposition of Mendelian inheritance. Proc. R. Soc. Edinburgh 52: 399–433.
Geritz S.A.H., Kisdi E., Meszena G., and Metz J.A.J. 1998. Evolutionarily singular strategies and the adaptive growth and branching of the evolutionary tree. Evol. Ecol. 12: 35–37.
Hacking I. 1965. The logic of statistical inference. Cambridge University Press, Cambridge.
Hacking I. 1975. The emergence of probability. Cambridge University Press, Cambridge.
Haldane J.B.S. 1932. The causes of evolution. Longmans, New York.
Hardy G.H. 1908. Mendelian proportions in a mixed population. Science 28: 49–50.
Harris T.E. 1963. The theory of branching processes. Springer Verlag, Berlin.
Hill W.G. 1984. Quantitative genetics, Part 1 (Benchmark Papers in Genetics). Van Nostrand Reinhold International, New York.
Kingsland S.E. 1985. Modeling nature: Episodes in the history of population ecology. University of Chicago Press, Chicago.
Lande R. 1979. Effective deme sizes during long-term evolution estimated from rates of chromosomal rearrangement. Evolution 33: 234–251.
May R.M. 1987. When two and two do not make four: Nonlinear phenomena in ecology. Proc. R. Soc. Lond. B 228: 241–266.
Otto S.P. and Day T. 2007. A biologist’s guide to mathematical modeling in ecology and evolution. Princeton University Press, Princeton, New Jersey.
Provine W. 1986. Sewall Wright and evolutionary biology. University of Chicago Press, Chicago.
Schär C. and Jendritsky G. 2004. Hot news from summer 2003. Nature 432: 559–560.
Schär C., Vidale P.L., Lüthi D., Frei C., Häberli C., Liniger M.A., and Appenzeller C. 2004. The role of increasing temperature variability in European summer heatwaves. Nature 427: 332–336.
Stachel J., ed. 1998. Einstein’s miraculous year: Five papers that changed the face of physics, pp. 71–98. Princeton University Press, New Jersey.
Stenseth N.C., Falck W., Chan K.S., Bjornstad O.N., O’Donoghue M., Tong H., Boonstra R., Boutin S., Krebs C.J., and Yoccoz N.G.. 1998. From patterns to processes: Phase and density dependencies in the Canadian lynx cycle. Proc. Natl. Acad. Sci. 95: 15430–15435.
Stigler S.M. 1999. Statistics on the table: The history of statistical concepts and methods. Harvard University Press, Cambridge, Massachusetts.
Waxman D. and Gavrilets S. 2004. 20 questions about adaptive dynamics. J. Evol. Biol. 18: 1139–1154.
Weinberg W. 1908. On the demonstration of heredity in man. Naturkunde in Wurttemberg, Stuttgart 64: 368–382.
|

