|
Problem 20.1
An insect can lay its eggs on two alternative host plants (A, B). However, there is a trade-off between the rate of survival on the two hosts, vA, vB, described by vA2 + vB2 ≤1 (Fig. P20.1). Thus, no genotype can survive well on both hosts: A genotype that can survive perfectly on A cannot survive on B (vA = 1, vB = 0; bottom right of Fig. 20.1), and vice versa; a generalist that can survive equally well on both cannot have survival greater than vA = vB = 1/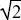 ~ 0.707. We can think of the survival on the two hosts as a phenotype that is described by the two numbers {vA, vB}. NOTE 20A ~ 0.707. We can think of the survival on the two hosts as a phenotype that is described by the two numbers {vA, vB}. NOTE 20A
|
| **i) |
Assume that there is no competition within host plants, so that an individual’s fitness is proportional to its survival. This is known as hard selection. If eggs are equally likely to be laid on A or B, what is the optimal survival vA, vB? If the chances of being laid on A, B are 7/31, 24/31, respectively, what is the optimal phenotype? HINT 20A
|
| *ii) |
Now, suppose that survival is fixed at vA = 0.6, vB = 0.8, but that the probability of laying eggs on host A, α, can vary. What is the optimal value of α? HINT 20B
|
| **iii) |
If both preference for where to lay eggs, α, and survival, {vA, vB}, can vary, what phenotype (or phenotypes) will evolve? HINT 20C
|
| ***iv) |
Now, suppose that there is intense competition within patches, so that the same fixed number of larvae emerge from each host plant. (This is known as soft selection see Fig. 18.22.) Now, the fitness of an individual depends on what the rest of the population is doing. For a fixed habitat preference, with eggs laid equally on the two hosts, show that the evolutionarily stable strategy (ESS) for survival, {vA, vB}, is a generalist strategy, where vA = vB = 1/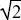 . NOTE 20B . NOTE 20B
|
| **v) |
What is the joint ESS, if both habitat preference, α, and survival, {vA, vB}, can vary? NOTE 20C
|
|
Problem 20.2
A sexually reproducing organism has an annual breeding season. It has a 50% chance of surviving to breed in the first year and then a 50% chance of surviving for each successive year.
|
| *i) |
Given that it survives, how many offspring must it produce each year in order to maintain a stable population?
|
| **ii) |
What selective advantage will an allele have that increases fecundity in the first year by 1%? What will be its advantage if it increases fecundity in year t?
|
| **iii) |
Answer the same question for an allele that increases survival by 1% from year t – 1 to year t.
|
|
Problem 20.3
An organism has a 50% chance of surviving to year 1; if it survives, it produces on average three offspring in that year. It then has a 20% chance of surviving to the next year, in which case it will produce an average of five offspring and then die.
|
| **i) |
Mutations occur that reduce fecundity in year 1 but have no other effect. (These mutations are not recessive.) The total rate of such mutations per diploid genome is U = 1, and their effects multiply together. By how much do such mutations reduce fecundity in year 1? By how much do they reduce overall relative fitness? HINT 20D
|
| **ii) |
Answer similar questions for mutations that only reduce fecundity in year 2.
|
| **iii) |
What will be the effects on fecundity and on net fitness of mutations that reduce fecundity in both years by the same proportion?
|
|
Problem 20.4
A species reproduces either in its first or second year; it has chance J of surviving to year 1, and then has chance A of surviving from the first year into the second. If it survives, it has the same fecundity in each of the first two years. The population size is regulated by a decrease in fecundity with increasing numbers; the population can be assumed to be stable.
Selection acts to increase both juvenile and adult survival. However, it is impossible for both to be maximized: there is a constraint that J + A4 < 1 (see Fig. P20.2).
|
| **i) |
What is the optimal life history? HINT 20E Does this optimal life history show senescence?
|
| *ii) |
What will be the selection coefficient against an allele that reduces juvenile survival, J, by 1%? What will be the selection coefficient against an allele that reduces adult survival, A, by 1%? HINT 20F NOTE 20D
|
|
Problem 20.5 *C28*
This problem examines a simple model for the joint evolution of a male trait and a female preference for that trait. The organism is haploid. A gene T determines the trait, with alleles TQ, TP at frequencies q, p (q + p = 1). Another gene, P, determines female preference and has two alleles PV, PU at frequencies v, u (v + u = 1). Females with PV mate at random, whereas females with PU only mate with males carrying TP. The two genes recombine at a rate c. Assume that all females produce the same number of offspring, so that there is no direct selection on the female preference gene, P. Assume also that the population is so large that PU females can always find TP males to mate with, even when TP is very rare.
|
| *i) |
How much does allele TP increase, as a result of sexual selection by the fraction u of females that prefer to mate with TP males? HINT 20G
|
| *ii) |
If TP is initially extremely rare, how frequent will it be after one generation of sexual selection?
|
| **iii) |
There is no direct selection on preference, P, because all females have the same fitness. However, if PU is associated (i.e., in linkage disequilibrium) with TP, then it will increase as TP increases. Suppose that the proportion of T alleles that are associated with PU is uP, and the fraction of TQ alleles that are associated with PU is uQ. (Thus, the overall frequency of PU is quQ + puP.) How much does the overall frequency of PU increase in a generation? HINT 20H
|
| ***iv) |
To complete the problem, we need to know the association between the two genes, uP – uQ. When the preference allele is rare (u << 1), it can be shown that this is close to uP – uQ = u/2p, independent of the recombination rate, c. Find by what factor the preference allele frequency, u, changes from one generation to the next, in terms of the change in the selected allele between generations (i.e., find ut + 1/ut in terms of pt + 1/pt). HINT 20I
|
| **v) |
Use this result to find how much the preference allele PU increases as the trait allele TP increases from very low frequency to fixation. HINT 20J NOTE 20E
|
|
Problem 20.6
This problem illustrates the handicap principle (see p. 581), by asking when male quality will be reliably associated with a sexually selected trait. Male deer with larger antlers survive less well but are more attractive to females. Males also vary in vigor, and antler size reduces the survival of the less vigorous males by more than it reduces the survival of the more vigorous males (see Fig. P20.3).
|
| *i) |
Plot net male fitness against antler size. HINT 20K
|
| **ii) |
What is the optimal antler size for a male of low quality? Of high quality? Sketch a graph of the optimal antler size against quality. HINT 20L
|
| *iii) |
Assuming that males display according to the optimal strategy, what fitness will they have? HINT 20M
|
| **iv) |
What will be the average fitness of offspring of females that choose to mate with males displaying different antler size? (A qualitative answer will be enough here.)
|

