Chapter 17 Notes
Selection on Variation
The Nature of Selection
Natural Selection Depends on Inherited Variation in Fitness
Darwin’s letters and notebooks have given us an extraordinarily detailed record of his thoughts. He came to the idea of natural selection as he read Malthus’ Essay on Population, between September 28 and October 3, 1838. Later, he came to use the term “natural selection,” and wrote out his ideas in his “Brief sketch” of May 1842. For a fascinating account, see Browne (1995, Chapters 16–18).
The quote is from Chapter 4 of Darwin (1859).
Figure 17.1 shows asexual reproduction (e.g., following the reproduction of individual genes).
Strictly speaking, selection can occur without any heritability; some individuals reproduce and some do not, and in that sense are “selected.” However, any evolutionary consequence—that is, any change in the following generation—does require that the fitness variation responsible for selection be heritable.
Selection Acts on Replicating Molecules
The example of in vitro selection on a ribozyme is from Lehman and Joyce (1993). See also Lehman et al. (2000).
Fitness Is Made Up of Separate Components
Figure 17.3B is from Woolhouse et al. (2001); the data for Figure 17.3 are courtesy of Louise Matthews, CTVM, Edinburgh. Background information can be found at http://footandmouth.csl.gov.uk/.
The definition of fitness in an age-structured population is given in more detail by Charlesworth (1980). For review, see Partridge and Barton (1993).
We show how fitness in an age-structured population can be using data from a laboratory population of Drosophila melanogaster (Roper et al. 1993).
The Increase in Mean Fitness Equals the Additive Genetic Variance in Fitness: Fisher’s Fundamental Theorem
Fisher sets out his Fundamental Theorem in Chapter 2 of The Genetical Theory of Natural Selection (1930). The theorem has often been misunderstood as making predictions about the total rate of change of mean fitness, but Fisher intended it as giving that part of the increase in mean fitness caused by the effect of selection on allele frequencies. Price (1972) and Ewens (1989, 1992, 1995) explain and justify this interpretation.
The quote from Fisher in Figure 17.4 is from The Genetical Theory of Natural Selection (1930). See http://www.economics.soton.ac.uk/staff/aldrich/fisherguide/quotations.htm.
We use the term “marginal effect” here to avoid distinguishing between average effect and average excess (p. 389). These are equivalent for random-mating populations and so, in this case, either can be used in . The Fundamental Theorem also applies with nonrandom mating, but care must be taken to use the appropriate definition of the additive variance.
Fisher’s Fundamental Theorem is a special case of a remarkably general equation, discovered independently by Robertson (1966) and Price (1970). This states that the change in the mean of any trait caused by selection is equal to the covariance of that trait with relative fitness (i.e., Δ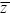 = cov(W/ = cov(W/ , z). Price (1970) added an extra term, which allows for the change in mean trait value during transmission between generations, hence giving an expression for the total change from one generation to the next. Price’s equation has become popular in recent years, especially for modeling social interactions (pp. 599–602). It is discussed in depth by Frank (1998). , z). Price (1970) added an extra term, which allows for the change in mean trait value during transmission between generations, hence giving an expression for the total change from one generation to the next. Price’s equation has become popular in recent years, especially for modeling social interactions (pp. 599–602). It is discussed in depth by Frank (1998).
Natural Selection Is the Only Process That Causes Adaptation
Depew and Weber (1995) give an interesting history of evolutionary thought and discuss self-organization in Chapters 16 and 18. They give the subject more importance than we do in Evolution.
Maynard Smith et al. (1985) give an excellent consensus view on the meaning and role of developmental constraints in evolution.
Darwin (1859) discusses the loss of unselected organs in Chapter 14 of On the Origin of Species. Loss of eyes in cave forms of Astyanax mexicanus is a classic example (Wilkens 1971), which was recently reexamined by Dowling et al. (2002) and Jeffery (2005). They found that eyelessness had evolved multiple times in caves, an example of convergent evolution.
Natural Selection Works Step by Step by Assembling Multiple Favorable Variations
The Library of Babel is by Borges (2000).
The word game in Figure 17.11 follows Bell (1997, pp. 21–22). Both Bell (1997, Chapter 1.10) and Dawkins (1986, Chapter 1; 1997) give excellent accounts of how natural selection builds up improbable structures step by step.
Lehman and Joyce’s (1993) experiment (Fig. 17.2) began by generating mutations with very high frequency (5% per site) in a 140-bp region. The initial population was so large, and the mutation rate so high, that it is likely that every four-base variant of the original sequence was present in multiple copies. However, the chance that a specific seven-base variant was present is very small. Thus, it is likely that the four variants that increased quickly (green curves) were present in the original population and that the other three mutations (blue and purple curves) arose later, by mutation of the four-variant sequence. Note that there is negligible recombination in this experiment, so that the fittest sequence must build up step by step (see Fig. 23.18). (This interpretation is courtesy of Lehman and Joyce; it is not spelled out in the original paper.) For discussion of this issue in the context of the evolution of novelty, see page 720.
Edwards (2000) gives a concise review of Fisher’s work. According to Edwards, the aphorism “Natural selection is a mechanism for generating an exceedingly high degree of improbability” was recorded first by Julian Huxley in 1936.
In the Genetical Theory, Fisher gave a nice rebuttal to “the objection which has been made, that the principle of Natural Selection depends on a succession of favourable chances” (Fisher 1930, p. 37):
The objection is more in the nature of an innuendo than of a criticism, for it depends for its force upon the ambiguity of the word chance, in its popular uses. The income derived from a Casino by its proprietor may, in one sense, be said to depend upon a succession of favourable chances, although the phrase contains a suggestion of improbability more appropriate to the hopes of the patrons of his establishment. It is easy without any very profound logical analysis to perceive the difference between a succession of favourable deviations from the laws of chance, and on the other hand, the continuous and cumulative action of these laws. It is on the latter that the principle of Natural Selection relies.”
Selection Is Often More Effective Than Rational Design
Kirkpatrick et al. (1983) review simulated annealing, with examples from chip design.
Holland (1975) introduced genetic algorithms; the field is now thriving (see, e.g., Mitchell 1998; Foster 2001; Landweber and Winfree 2002) but has remained separate from evolutionary biology.
Lipson and Pollack (2000) give an interesting example of the evolution of novel designs of . Supplements to this journal article include several amusing videos of the evolved robots. Also see http://demo.cs.brandeis.edu/pr/robotics.html.
Figure 17.13 is from Koza et al. (2002).
Even Slight Differences in Fitness Eventually Become Significant
Haldane set out the basic population genetics of selection in a series of papers in the 1920s and 1930s. These are summarized in his Causes of Evolution (1932).
Haldane and Jayakar (1963) showed that the outcome of fluctuating selection depends on the geometric mean fitness.
The Fitness of a Gene Depends on Interactions with the Physical and Biotic Environment and with Other Genes
The evidence that the melanic form of Biston betularia is selected via bird predation is reviewed by Majerus (1998). His criticisms of some of Kettlewell’s early experiments on differential predation attracted much attention, following a review of his book by Coyne (1998). However, differential predation has been observed in many later studies. For a review of the controversy, see Majerus (2005).
The idea that fitnesses depend on genotype frequency is well established in population genetics (see, e.g., Clarke 1972) and reappears in various guises, especially in game theory and social evolution, which are covered in Chapters 20 and 21.
Populations Evolve to Peaks on the Adaptive Landscape
Sewall Wright (1931, 1932) introduced the metaphor of the adaptive landscape and quantified it in a series of subsequent theoretical papers. Specifically, he showed that selection changes allele frequency at a rate proportional to the gradient of the adaptive landscape and that in the presence of random drift, allele frequencies cluster around adaptive peaks (Chapter 18, pp. 494–496). Wright’s collected papers (Provine 1986a) are accompanied by useful commentaries.
The Metaphor of an Adaptive Landscape Can Be Misleading
Provine (1986b, Chapter 9) gives an excellent critique of Wright’s ideas; in particular, he points out that Wright switched between the two versions of the adaptive landscape mentioned in the text without ever discussing the distinction between them. (For Wright’s reply [written 55 years after he introduced fitness landscapes], see Wright 1988.) Individual fitness can be seen as a function of individual genotype (see Fig. 17.12), or population mean fitness can be seen as a function of allele frequencies (see Fig. 17.21) or trait means (see Fig. 17.27). One reason for preferring the latter version is that it gives a quantitative result: The rate of change of allele frequencies is proportional to the gradient of mean fitness with respect to allele frequencies.
Müllerian Mimicry Favors Common Color Patterns
Turner (1981) and Mallet and Joron (1999) review Müllerian mimicry in Heliconius butterflies. Sheppard (1975) gives an excellent account of the older literature.
Selection on Quantitative Traits
Selection Acts in a Simple Way on Quantitative Traits
Grant (1986, Chapter 8) summarizes studies of natural selection on the Galápagos finches.
The figure for the response to selection on bill depth of “about 0.6 standard deviations” is derived from data in Grant (1986) as follows: The mean coefficient of variation (i.e., s.d./mean) is 0.0704 (Grant’s Table 7), the mean bill depth is about 10 mm (Grant’s Fig. 55), and the evolutionary response is about 4% (0.4 mm). Hence in s.d., it is 0.4/0.7 = 0.57 s.d.
Selection Changes Quantitative Traits at a Rate Proportional to Their Additive Genetic Variance
There is a subtlety in the use of the selection gradient, which none of the textbooks address (Falconer and Mackay [1995] and Roff [1997] give the selection gradient cursory treatment). Essentially, it is the confusion noted by Provine (1986b) between the two versions of the adaptive landscape (see above). The regression of individual fitness on trait is not quite the same as the regression of mean fitness on trait mean. The rate of change of the population can be written as proportional to either dlog( )/d )/d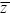 or to the usual selection gradient β, which is defined as the regression of relative individual fitness on trait. These are the same only if the distribution is normal. In addition, there is disagreement over whether one regresses log fitness on trait value or regresses raw fitness and divides by mean fitness. All of these versions are approximately the same when selection is weak, however. or to the usual selection gradient β, which is defined as the regression of relative individual fitness on trait. These are the same only if the distribution is normal. In addition, there is disagreement over whether one regresses log fitness on trait value or regresses raw fitness and divides by mean fitness. All of these versions are approximately the same when selection is weak, however.
Figure 17.27 is from Moore (1990). The figure shows a quadratic fit to field data. This is not quite satisfactory, because it gives negative fitness estimates within the range of the data. Schluter and Nychka (1994) give a method that estimates fitness landscapes that does not assume (say) a quadratic form and so avoids this difficulty; see Brodie et al. (1995). We discuss methods for estimating selection on quantitative traits on pages 525–530.
We have given formulae for the change in the mean value of a quantitative trait (Equation 17.3) and for the change in allele frequency (Box 17.1). The relation between changes in quantitative traits and changes in allele frequency is in more detail.
Selection on One Trait Causes Changes in Other Traits That Are Genetically Correlated with It
Falconer and Mackay (1995, Chapter 19) explain selection on correlated traits.
Artificial Selection Usually Produces a Rapid and Continued Response
Diamond (1998) gives a fascinating account of the importance of domestication of plants and animals to human history.
Figure 17.30 is from a survey by Gingerich (1983). Long-term rates are slower because they average over faster short-term fluctuations.
The Illinois corn experiment is reviewed in a special issue of Plant Breeding Reviews (2004; 24(1)). The genetic basis of the selection response is analyzed by Laurie et al. (2004); this and other recent work is summarized by Hill (2005). Figure 17.31A is redrawn from Figure 5.1 of Dudley and Lambert (2004).
The experiment is by Weber (1996). Marden et al. (1997) analyze the physiological basis of improved flying ability.
Long-term selection experiments in Escherichia coli are reviewed by Lenski et al. (1998). Figure 17.32 is from Lenski and Travisano (1994).
Additive Genetic Variance Remains High Despite Continued Selection
Barton and Keightley (2002) review alternative explanations for sustained and replicable long-term selection responses. See also Hill (2005) and Keightley (2004).
Figure 17.34 is redrawn from Yoo (1980).
Hill (1982) made an influential argument for the importance of mutation in sustaining the response to artificial selection.
The infinitesimal model is discussed by Lynch and Walsh (Chapter 15 of http://nitro.biosci.arizona.edu/zbook/volume_2/vol2.html). With a very large number of additive alleles, each of very small effect, selection changes the mean but does not eliminate the genetic variance. This model is equivalent to assuming that offspring have breeding values that are normally distributed about the mid-parental value, with constant variance (see Problem 23.8).
McKenzie and Batterham (1994) review evidence for the evolution of modifiers that ameliorate initially deleterious pleiotropic side effects.
Keightley (2004) compares selection response from inbred and outbred base populations.
Selection on Multiple Genes
When Genes Are Associated with Each Other in Linkage Disequilibrium, Selection on One Gene Causes Changes at Others
Haldane (1964) gave a vigorous defense of “bean-bag genetics.”
Figure 17.35 is redrawn from Clegg et al. (1976).
Several Processes Can Generate Linkage Disequilibrium
Figure 17.36B is redrawn from Berry et al. (1991).
For details of Batesian mimicry, see Sheppard (1975).
References
Barton N.H. and Keightley P.D. 2002. Understanding quantitative genetic variation. Nat. Rev. Genet. 3: 11–21.
Bell G. 1997. Selection: The mechanism of evolution. Chapman and Hall, New York.
Berry R.J., Triggs G.S., King P., Nash H.R., and Noble L.R. 1991. Hybridization and gene flow in house mice introduced into an existing population on an island. J. Zool. 225: 615–632.
Borges J.L. 2000. Labyrinths: Selected stories and other writings. Penguin Modern Classics, New York. (First published in Spanish, 1941.)
Brodie E.D., Moore A.J., and Janzen F.J. 1995. Visualizing and quantifying natural selection. Trends Ecol. Evol. 10: 313–319.
Browne E.J. 1995. Charles Darwin: Voyaging, Volume 1 of a Biography. Jonathan Cape, London.
Charlesworth B. 1980. Evolution in age-structured populations. Cambridge University Press, Cambridge.
Clarke B.C. 1972. Density-dependent selection. Am. Nat. 106: 1–13.
Clegg M.T., Kidwell J.F., Kidwell M.G., and Daniel N.J. 1976. Dynamics of correlated genetic systems. I. Selection in the region of the glued locus of Drosophila melanogaster. Genetics 83: 793–810.
Coyne J.A. 1998. Not black and white. Nature 396: 35–36.
Darwin C. 1859. On the origin of species by means of natural selection. John Murray, London.
Dawkins R. 1986. The blind watchmaker. Longman, London.
Dawkins R. 1997. Climbing mount improbable. Penguin Science. London.
Depew D.J. and Weber B.H. 1995. Darwinism evolving. MIT Press, Cambridge, Massachusetts.
Diamond J. 1998. Guns, germs and steel. Vintage, New York.
Dowling T.E., Martasian D.P., and Jeffery W.R. 2002. Evidence for multiple genetic forms with similar eyeless phenotypes in the blind cavefish, Astyanax mexicanus. Mol. Biol. Evol. 19: 446–455.
Dudley J. and Lambert R.J. 2004. 100 generations of selection for oil and protein in corn. Plant Breed. Rev. 24: 79–110.
Edwards A.W.F. 2000. The genetical theory of natural selection. Genetics 154: 1419–1426.
Ewens W.J. 1989. An interpretation and proof of the Fundamental Theorem of Natural Selection. Theor. Popul. Biol. 36: 167–180.
Ewens W.J. 1992. An optimizing principle of natural selection in evolutionary population genetics. Theor. Popul. Biol. 42: 333–346.
Ewens W.J. 1995. Addendum to “The fundamental theorem of natural selection in Ewens’ sense (case of many loci)” by Castilloux and Lessard. Theor. Popul. Biol. 48: 316–317.
Falconer D.S. and Mackay T.F.C. 1995. Introduction to quantitative genetics. Longman, London.
Fisher R.A. 1930. The genetical theory of natural selection. Oxford University Press, Oxford.
Foster J.A. 2001. Evolutionary computation. Nat. Rev. Genet. 2: 428–436.
Frank S.A. 1998. Foundations of social evolution. Princeton University Press, Princeton, New Jersey.
Gingerich P.D. 1983. Rates of evolution: Effect of time and temporal scaling. Science 222: 159–161.
Grant P.R. 1986. The evolution and ecology of Darwin’s finches. Princeton University Press, Princeton, New Jersey.
Haldane J.B.S. 1932. The causes of evolution. Longmans, New York.
Haldane J.B.S. and Jayakar S.D. 1963. Polymorphism due to selection of varying direction. J. Genet. 58: 237–242.
Haldane J.B.S. 1964. A defense of beanbag genetics. Perspect. Biol. Med. 7: 343–359.
Hill W.G. 1982. Rates of change in quantitative traits from fixation of new mutations. Proc. Natl. Acad. Sci. 79: 142–145.
Hill W.G. 2005. A century of corn selection. Science 307: 683–685.
Holland J.H. 1975. Adaptation in natural and artificial systems. University of Michigan Press, Ann Arbor.
Jeffery W.R. 2005. Adaptive evolution of eye degeneration in the Mexican blind cavefish. J. Hered. 96: 185–196.
Keightley P.D. 2004. Mutational variation and long-term selection response. Plant Breed. Rev. 24: 227–247.
Kirkpatrick S., Gelatt C.D., and Vecchi M.P. 1983. Optimization by simulated annealing. Science 220: 671–680.
Koza J.R., Bennett F.H., Andre D., and Keane M.A. 2002. Genetic programming: biologically inspired computation that creatively solves non-trivial problems. In Evolution as computation (ed. L.F. Landweber and A.T. Winfree). Springer-Verlag, Berlin.
Landweber L.F. and A. T. Winfree, eds. 2002. Evolution as Computation. Springer-Verlag, Berlin.
Laurie C.C., Chasalow S.D., Ledeaux J.R., McCarroll R., Bush D., et al. 2004. The genetic architecture of response to long-term artificial selection for oil concentration in the maize kernel. Genetics 168: 2141–2155.
Lehman N., Delle Donne M., West M., and Dewey T.G. 2000. The genotypic landscape during in vitro evolution of a catalytic RNA: Implications for phenotypic buffering. J. Mol. Evol. 50: 481–490.
Lehman N. and Joyce G.F. 1993. Evolution in vitro: Analysis of a lineage of ribozymes. Curr. Biol. 3: 723–734.
Lenski R.E. and Travisano M. 1994. Dynamics of adaptation and diversification: A 10,000 generation selection experiment with bacterial populations. Proc. Natl. Acad. Sci. 91: 6608–6618.
Lenski R.E., Mongold J.A., Sniegowski P.D., Travisano M., Vasi F., et al. 1998. Evolution of competitive fitness in experimental populations of Escherichia coli: What makes one genotype a better competitor than another? Antonie Van Leeuwenhoek 73: 35–47.
Lipson H. and Pollack J.B. 2000. Automatic design and manufacture of robotic life forms. Nature 406: 974–978.
Lynch M. and Walsh B. Genetics and analysis of quantitative traits. http://nitro.biosci.arizona.edu/zbook/volume_2/vol2.html.
Majerus M.E.N. 1998. Melanism: Evolution in action. Oxford University Press, Oxford.
Majerus M.E.N. 2005. The peppered moth: Decline of a Darwinian disciple. In Insect evolutionary biology (ed. M.D.E. Fellowes et al.). CABI Publishing, Wallingford, United Kingdom.
Mallet J.L.B. and Joron M. 1999. Evolution of diversity in warning color and mimicry: Polymorphisms, shifting balance, and speciation. Annu. Rev. Ecol. Syst. 30: 201–233.
Marden J.H., Wolf M.R., and Weber K.E. 1997. Aerial performance of Drosophila melanogaster from populations selected for upwind flight ability. J. Exp. Biol. 200: 2747–2755.
Maynard Smith J., Burian R., Kauffman S., Alberch P., Campbell J., et al. 1985. Developmental constraints and evolution. Q. Rev. Biol. 60: 265–287.
McKenzie J.A. and Batterham P. 1994. The genetic, molecular and phenotypic consequences of selection for insecticide resistance. Trends Ecol. Evol. 9: 166–170.
Mitchell M. 1998. An introduction to genetic algorithms. MIT Press, Cambridge, Massachusetts.
Moore A.J. 1990. The evolution of sexual dimorphism by sexual selection—The separate effects of intrasexual selection and intersexual selection. Evolution 44: 315–331.
Partridge L. and Barton N.H. 1993. Optimality, mutation and the evolution of ageing. Nature 362: 305–311.
Price G.R. 1970. Selection and covariance. Nature 227: 520–521.
Price G.R. 1972. Fisher’s “Fundamental Theorem” made clear. Ann. Hum. Genet. 36: 129–140.
Provine W. 1986a. Evolution: Collected papers of S. Wright. University of Chicago Press, Chicago.
Provine W. 1986b. Sewall Wright and evolutionary biology. University of Chicago Press, Chicago.
Robertson A. 1966. A mathematical model of the culling process in dairy cattle. Anim. Prod. 8: 95–108.
Roff D.A. 1997. Evolutionary quantitative genetics. Chapman and Hall, New York.
Roper C., Pignatelli P., and Partridge L. 1993. Evolutionary effects on age at reproduction in larval and adult Drosophila melanogaster. Evolution 47: 445–455.
Schluter D. and Nychka D. 1994. Exploring fitness surfaces. Am. Nat. 143: 597–616.
Sheppard P.M. 1975. Natural selection and heredity, 4th ed. Hutchinson, London.
Turner J.R.G. 1981. Adaptation and evolution in Heliconius: A defence of neo-Darwinism. Annu. Rev. Ecol. Syst. 12: 99–122.
Weber K.E. 1996. Large genetic change at small fitness cost in large populations of Drosophila melanogaster selected for wind tunnel flight: Rethinking fitness surfaces. Genetics 144: 205–213.
Wilkens H. 1971. Genetic interpretation of regressive evolutionary processes: Studies on hybrid eyes of two Astyanax cave populations (Characidae, Pisces). Evolution 25: 530–544.
Woolhouse M., Chase-Topping M., Haydon D., Friar J., Matthews L. et al. 2001. Foot-and-mouth disease under control in the UK. Nature 411: 258–259.
Wright S. 1931. Evolution in Mendelian populations. Genetics 16: 97–159.
Wright S. 1932. The roles of mutation, inbreeding, crossbreeding and selection in evolution. Proc. Sixth Int. Congr. Genet. 1: 356–366.
Wright S. 1988. Surfaces of selective value revisited. Am. Nat. 131: 115–123.
Yoo B.H. 1980. Long-term selection for a quantitative character in large replicate populations of Drosophila melanogaster. I. Response to selection. Genet. Res. 35: 1–17.
|

